Problem 3 Temperature distribution in a hot-wire anemometer. A hot-wire anemometer is essentially a fine wire, usually made of platinum, which is heated electrically and exposed to a flowing fluid. Its temperature, which is a function of the fluid temperature, fluid velocity, and the rate of heating, may be determined by measuring its electrical resistance. It is used for measuring velocities and velocity fluctuations in flow systems. In this problem we analyze the temperature distribution in the wire element. We consider a wire of diameter D and length 2L supported at its ends (z = -L and z =+L) and mounted perpendicular to an air stream. An electric current of density I amp/cm² flows through the wire, and the heat thus generated is partially lost by convection to the air stream and partially by conduction toward the ends of the wire. Because of their size and their high electrical and thermal conductivity, the supports are not appreciably heated by the current, but remain at the temperature TL, which is the same as that of the approaching air stream. Heat loss by radiation is to be neglected. (a) Derive an equation for the steady-state temperature distribution in the wire, assuming that I depends on z alone; that is, the radial temperature variation in the wire is neglected. Further, assume uniform thermal and electrical conductivities (k and ke) in the wire, and a uniform heat transfer coefficient h from the wire to the air stream. (b) Compute the current, in amperes, required to heat a platinum wire to a midpoint temperature of 50°C under the following conditions: TL = 20°C D = 0.127 mm L = 0.5 cm h = 100 Btu/hr ft².°F k= 40.2 Btu/hr ft.°F ke 1.00 x 105 ohm ¹cm¹ -1 =
Problem 3 Temperature distribution in a hot-wire anemometer. A hot-wire anemometer is essentially a fine wire, usually made of platinum, which is heated electrically and exposed to a flowing fluid. Its temperature, which is a function of the fluid temperature, fluid velocity, and the rate of heating, may be determined by measuring its electrical resistance. It is used for measuring velocities and velocity fluctuations in flow systems. In this problem we analyze the temperature distribution in the wire element. We consider a wire of diameter D and length 2L supported at its ends (z = -L and z =+L) and mounted perpendicular to an air stream. An electric current of density I amp/cm² flows through the wire, and the heat thus generated is partially lost by convection to the air stream and partially by conduction toward the ends of the wire. Because of their size and their high electrical and thermal conductivity, the supports are not appreciably heated by the current, but remain at the temperature TL, which is the same as that of the approaching air stream. Heat loss by radiation is to be neglected. (a) Derive an equation for the steady-state temperature distribution in the wire, assuming that I depends on z alone; that is, the radial temperature variation in the wire is neglected. Further, assume uniform thermal and electrical conductivities (k and ke) in the wire, and a uniform heat transfer coefficient h from the wire to the air stream. (b) Compute the current, in amperes, required to heat a platinum wire to a midpoint temperature of 50°C under the following conditions: TL = 20°C D = 0.127 mm L = 0.5 cm h = 100 Btu/hr ft².°F k= 40.2 Btu/hr ft.°F ke 1.00 x 105 ohm ¹cm¹ -1 =
Related questions
Question

Transcribed Image Text:Problem 3
Temperature distribution in a hot-wire anemometer. A hot-wire anemometer is essentially a fine
wire, usually made of platinum, which is heated electrically and exposed to a flowing fluid. Its
temperature, which is a function of the fluid temperature, fluid velocity, and the rate of heating,
may be determined by measuring its electrical resistance. It is used for measuring velocities and
velocity fluctuations in flow systems. In this problem we analyze the temperature distribution in
the wire element.
We consider a wire of diameter D and length 2L supported at its ends (z = -L and z=+L)
and mounted perpendicular to an air stream. An electric current of density I amp/cm² flows
through the wire, and the heat thus generated is partially lost by convection to the air stream and
partially by conduction toward the ends of the wire. Because of their size and their high electrical
and thermal conductivity, the supports are not appreciably heated by the current, but remain at
the temperature TL, which is the same as that of the approaching air stream. Heat loss by
radiation is to be neglected.
(a) Derive an equation for the steady-state temperature distribution in the wire, assuming that I
depends on z alone; that is, the radial temperature variation in the wire is neglected. Further,
assume uniform thermal and electrical conductivities (k and ke) in the wire, and a uniform heat
transfer coefficient h from the wire to the air stream.
(b) Compute the current, in amperes, required to heat a platinum wire to a midpoint temperature
of 50°C under the following conditions:
TL = 20°C
D = 0.127 mm
L = 0.5 cm
h = 100 Btu/hr ft².°F
k = 40.2 Btu/hr-ft-°F
ke 1.00 x 105 ohm¹¹cm¹
Expert Solution
Step 1
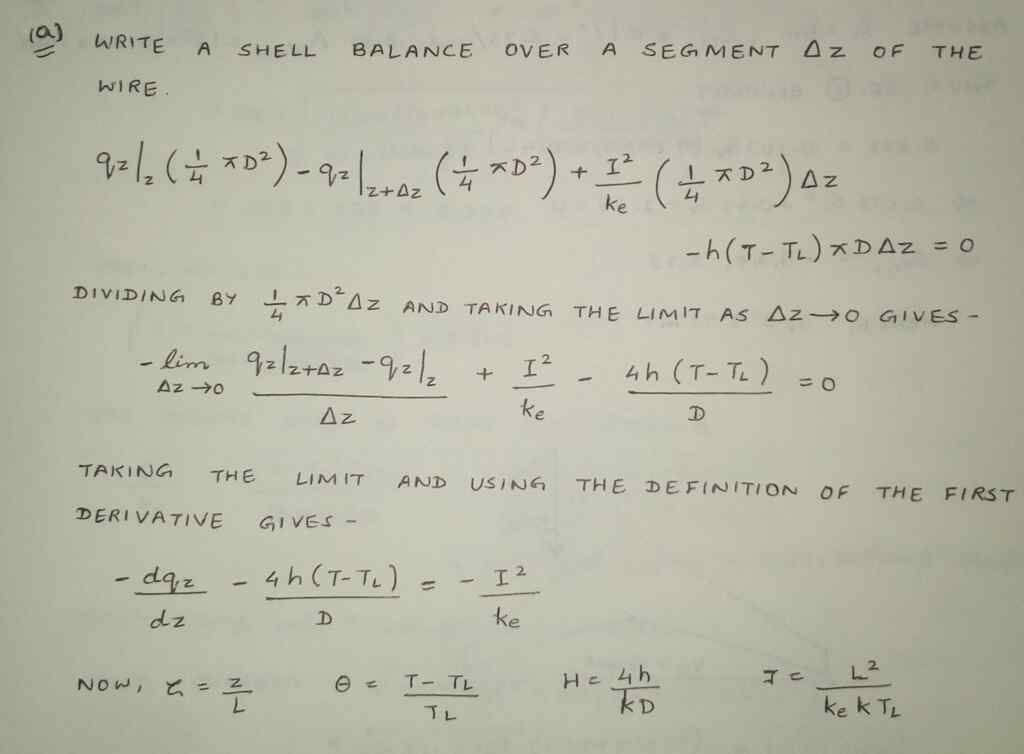
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images
