Problem 2: A block with a mass of m = 1.5 kg rests on a wooden plank. The coefficient of static friction between the block and the plank is u, = 0.78. One end of the board is attached to a hinge so that the other end can be lifted forming an angle, 0, with respect to the ground. Assume the x-axis is along the plank as shown in the figure.
Problem 2: A block with a mass of m = 1.5 kg rests on a wooden plank. The coefficient of static friction between the block and the plank is u, = 0.78. One end of the board is attached to a hinge so that the other end can be lifted forming an angle, 0, with respect to the ground. Assume the x-axis is along the plank as shown in the figure.
Related questions
Question
Answer question 2 parts d-f

Transcribed Image Text:Problem 2: A block with a mass of m = 1.5 kg rests on a wooden plank. The
coefficient of static friction between the block and the plank is u, = 0.78. One end of
the board is attached to a hinge so that the other end can be lifted forming an angle, 0,
with respect to the ground. Assume the x-axis is along the plank as shown in the figure.
Part (a)
Fs for the force of static friction, and Fk for the force of kinetic friction.
FBD :
draw the Free Body Diagram for this block, assuming it is in static equilibrium. If necessary, use
Force Labels:
Fn, Fg, Fs, Fk, a, v
45,0, 90, 135, 180, 225, 270, 315, 0
Angle Labels:
Part (b) Assuming the x-direction is along the plank as shown, find an expression for the magnitude of the force of gravity in the y-direction, Fey,
perpendicular to the plank in terms of given quantities and variables available in the palette.
Expression :
gy
Select from the variables below to write your expression. Note that all variables may not be required.
acotan(u,), atan(u,), cos(a), cos(), cos(0), sin(a), sin(o), sin(0), tan(0), a, ß, uk, Us, 0, b, d, g, h, m, t
Part (c) Write an expression for the magnitude of the maximum friction force along the surface, F,, in terms of given quantities and variables
available in the palette.
Expression :
F =
Select from the variables below to write your expression. Note that all variables may not be required.
acotan(us), atan(us), cos(a.), cos(4), cos(0), sin(a), sin(4), sin(0), a, µk, µs, b, g, m, t
Part (d) Assuming the static friction is maximized, write an expression, using only the given parameters and variables available in the palette, for
Page

Transcribed Image Text:Part (b) Assuming the x-direction is along the plank as shown, find an expression for the magnitude of the force of gravity in the y-direction, Fgy,
perpendicular to the plank in terms of given quantities and variables available in the palette.
Expression :
F
gy
Select from the variables below to write your expression. Note that all variables may not be required.
acotan(u,), atan(u,), cos(a), cos(4), cos(0), sin(a), sin(4), sin(0), tan(0), a, ß, µk, µs, 0, b, d, g, h, m, t
Part (c) Write an expression for the magnitude of the maximum friction force along the surface, F, in terms of given quantities and variables
available in the palette.
Expression :
Fs =
Select from the variables below to write your expression. Note that all variables may not be required.
acotan(us), atan(u,), cos(a), cos(4), cos(0), sin(a), sin(o), sin(0), a., µk, µs, b, g, m, t
Part (d) Assuming the static friction is maximized, write an expression, using only the given parameters and variables available in the palette, for
the sum of the forces along the plank, EF..
Expression :
EF x
Select from the variables below to write your expression. Note that all variables may not be required.
acotan(u,), atan(u,), cos(a), cos(4), cos(0), sin(a), sin(4), sin(0), a., µk, µs, b, g, m, t
Part (e) Write an expression for the maximum angle, 0m, that the board can make with respect to the horizontal before the block starts moving.
(Write in terms of the given parameters and variables available in the palette.)
Expression :
Om
Select from the variables below to write your expression. Note that all variables may not be required.
acotan(u), atan(µ,), cos(a), cos(4), cos(0), sin(a), sin(4), sin(0), tan(0), a, µk, µs, 0, b, t
Part (f) Solve numerically for the maximum angle, 0m, in degrees.
Numeric : A numeric value is expected and not an expression.
Om =
Expert Solution
Step 1
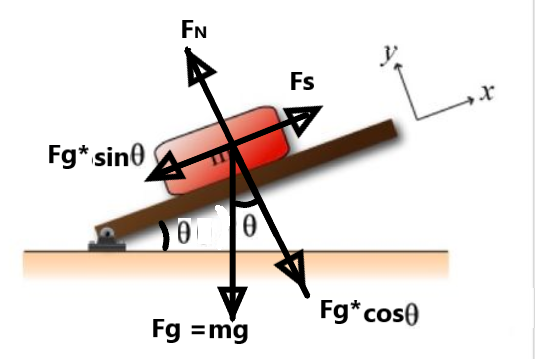
a.
When the object is placed upon an inclined plane, the angle at which the object just starts to slide down is called the angle of repose.
The weight of the object acts vertically downward and that mg can be resolved into two components mgsin parallel to the plane and mgcos normal to it.
The component mgcos balances the normal reaction and the component mgsin is balanced by the frictional force.
The FBD for the static equilibrium condition is,
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 6 images
