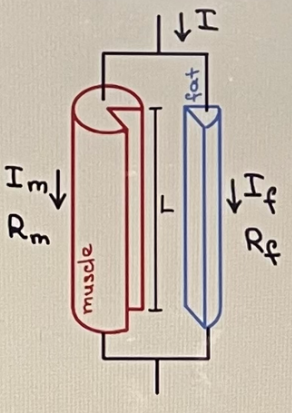
Problem 1: The conductive tissues of the upper leg can be modeled as a 40-cm-long, 12-cm-diameter cylinder of muscle and fat. The resistivities of muscle and fat are Pm = 13 22 m and pf = 25 22 m, respectively. One person's upper leg is 82% muscle, 18% fat. What current is measured if a AV = 1.5 V potential difference is applied between the person's hip and knee? a) Model the muscle and fat tissues as separate segments of the cylin- der connected as shown in Fig.1. The segments have the same length L but different cross sectional areas, based on their percentages. Compute separately the resistances of the muscle and the fat tissues, Rm and Rf.
Problem 1: The conductive tissues of the upper leg can be modeled as a 40-cm-long, 12-cm-diameter cylinder of muscle and fat. The resistivities of muscle and fat are Pm = 13 22 m and pf = 25 22 m, respectively. One person's upper leg is 82% muscle, 18% fat. What current is measured if a AV = 1.5 V potential difference is applied between the person's hip and knee? a) Model the muscle and fat tissues as separate segments of the cylin- der connected as shown in Fig.1. The segments have the same length L but different cross sectional areas, based on their percentages. Compute separately the resistances of the muscle and the fat tissues, Rm and Rf.
Related questions
Question

Transcribed Image Text:=
Problem 1: The conductive tissues of the upper leg can be modeled as a
40-cm-long, 12-cm-diameter cylinder of muscle and fat. The resistivities
of muscle and fat are pm = 132 m and pf 25 2 m, respectively. One
person's upper leg is 82% muscle, 18% fat. What current is measured if a
AV = 1.5 V potential difference is applied between the person's hip and
knee?
a) Model the muscle and fat tissues as separate segments of the cylin-
der connected as shown in Fig.1. The segments have the same length L
but different cross sectional areas, based on their percentages. Compute
separately the resistances of the muscle and the fat tissues, Rm and Rf.
Im↓
Rm
muscle
↓I
R&
FIG. 1: The scheme for Problem 1
Expert Solution
Step 1
Given that:
Step by step
Solved in 2 steps with 1 images
