Of the following options for the objective function, which is correct for this LP? O O min z = 24 Σ²=1 Σ¼=1 Xij * Xi+1,j+1 + 36 Σi=1 Σj=1 Xij * Xi+2,j+2 2= = 24(X12 + X14 + X23 + X34 +X13 + X24) min Z= 216(x12 + x14 + X23 + X34) + 144(x13 + X24) 2 = 144(x12 + x14 + X23 +X34) + 216(x13 + X24) 216(x12 +14+x23 + x34) +144(x13 + x24) max z = 12²₁₁ Σj=1 Xij * Xi+1,j+1 + 18 Σi=1 Σj=1 Xij * Xi+2,j+2 =1 max min max z =
Of the following options for the objective function, which is correct for this LP? O O min z = 24 Σ²=1 Σ¼=1 Xij * Xi+1,j+1 + 36 Σi=1 Σj=1 Xij * Xi+2,j+2 2= = 24(X12 + X14 + X23 + X34 +X13 + X24) min Z= 216(x12 + x14 + X23 + X34) + 144(x13 + X24) 2 = 144(x12 + x14 + X23 +X34) + 216(x13 + X24) 216(x12 +14+x23 + x34) +144(x13 + x24) max z = 12²₁₁ Σj=1 Xij * Xi+1,j+1 + 18 Σi=1 Σj=1 Xij * Xi+2,j+2 =1 max min max z =
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:Every day, secret, over-worked employees at Wayne Enterprises work two 6-hour shifts producing Batmobiles. These
shifts are selected from 12 am - 6 am, 6 am - 12 pm, 12 pm - 6 pm, and 6 pm - 12 am. The following table depicts the
number of employees needed during each shift:
Shift Time Period
1
2
3
4
12 am - 6 am
6 am - 12 pm
12 pm - 6 pm
6 pm - 12 am
Number of Employees Required
13
21
17
11
Bruce Wayne pays all employees working two consecutive shifts, $12 per hour (Note: employees scheduled to work
12 am - 6 am and 6 pm - 12 am would be considered consecutive). Employees whose shifts are not consecutive are
paid $18 per hour for the inconvenience.
Formulate an LP that can be used to minimize the cost of meeting the daily workforce demands for Batmobile
production.
To formulate the model, use the following decision variables:
Xij
= workers working shifts i and j where i, j = {1, 2, 3, 4}

Transcribed Image Text:Of the following options for the objective function, which is correct for this LP?
O min 2 =
min
max 2 = 24(x12 + X14 + X23 + X34 + X13 + X24)
min z = 216(x12 + x14 + X23 + X34) + 144(X13 + X24)
* = 144(x12 + x14 + X23 + X34) +216(x13 + X24)
216(x12 + X14 + X23 + X34) + 144(x13 + X24)
12 Σ
max
max
z =
24Σ 1Σ=1&ij*Wi+1+1+ 36
ΣΣ=1&ij*Wi+23+2
•j=1
* Ξ
4
i=1
Σ
=1 Wij * Wi+1,j+1 + 18 Σ 1 Σ=1ij * Xi+2,j+2
i=1
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 3 steps with 3 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
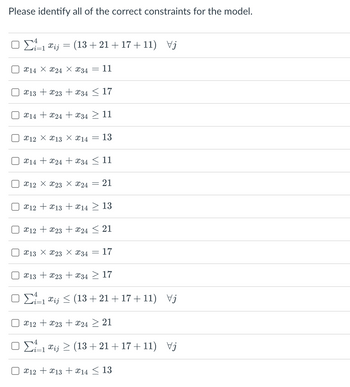
Transcribed Image Text:Please identify all of the correct constraints for the model.
ΟΣ=1&i
U
Π
U
Π
Π
Π
=
Π
(13 + 21 + 17 + 11) Vj
214 Χ 224 Χ 234
X13 + x23 +34 ≤ 17
11
X14X24 + X34 ≥ 11
212 Χ 213 Χ 214 = 13
X14X24X34 ≤ 11
€12 Χ 223 Χ 224
=
21
x12 +13 + 14 ≥ 13
X12 + x23 + x24 ≤ 21
213 Χ 223 Χ 34 17
x13x23x34 ≥ 17
ΟΣ=1&ij < (13 + 21 + 17 + 11) Va
X12 + x23 + x24 ≥ 21
ΟΣ=1 €i; > (13 + 21 + 17 + 11) Vj
x12 + x13 + 14 ≤ 13
Solution
Follow-up Question

Transcribed Image Text:Which statement represents the correct sign restriction for our decision variable?
It is not necessary to include a sign restriction.
X12, 14, X23, X34 0
X13, X240
Xij ≤0 Vi, j
xįj urs (unrestricted) Vi, j
xij≥0 Vi, j
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

