Please derive the attatched velocity transformations by using the Lorentz transformation for the velocity four vector (uμ). (hint: two of the Lorentz transformation equations are needed to solve this)
Q: For what value of υ does γ = 1.010 0? Observe that for speeds lower than this value, time dilation…
A: It is given that,
Q: In a certain inertial frame two light pulses are emitted, a distance 5 km apart and separated by 5…
A:
Q: Alice, an inertial observer, see Bob undergoing hyperbolic motion given by the parametric equations…
A: This question is a physics problem that involves analyzing the motion of an object, Bob, from the…
Q: The frame is generally understood to be the frame in which the target is at rest. True or False?…
A: It is required to identify whether the given statement is true or false.
Q: E 1. Two inertial frames S and S' move in standard configuration with respect to each other, with…
A: According to Einstein's Special Theory of Relativity it is practically impossible to say in absolute…
Q: Derive the Lorentz transformation connecting a frame SS (the lab frame) to a frame S′S′ that moves…
A: When a frame of reference is in motion with respect to another frame of reference, the observations…
Q: The contraction p'u¡, where p' is the four-momentum and u' is the four-velocity, is:
A: The four-momentum is given by pi = mui Where m = mass of the particle The four-velocity is…
Q: Find the matrix for the Lorentz transformation consisting a boost Vx in the x- direction followed by…
A:
Q: 6. Cathy has a “yardstick" that she thinks is 1 unit of distance long, which she holds in what she…
A:
Q: alculate the interval Δs2 between two events with coordinates (x1 = 55m, y1 = 0m, z1 = 0m, t1 = 1…
A:
Q: Galilean relativity: A woman standing still at a train station watches two girls throwing a tennis…
A:
Q: z²+zí+z*+z¹z³ #ziz+zık +zıx + zitza
A: We know that by Lorentz equation for a moving inertial frame with velocity v with respect to a other…
Q: (a) Since the four-velocity u = Yu (c, u) is a four-vector, you should immediately know what its…
A:
Q: Learning Goal: To be able to perform Lorentz transformations between inertial reference frames.…
A: Step 1 : According to Lorentz transformations, the time in s' frame, which is moving with a speed v…
Q: Show that the following form of Newton's second law satisfies the Lorentz transformation. Assume the…
A:
Q: In frame S, a particle of mass M travels along the x-axis with velocity v. It decays into two…
A: Let the rest frame of particle of mass M be S'. S' is moving be moving at velocity v along x axis…
Q: A relativistic particle of charge q and massm,moves under the action of a constant electric field of…
A:
Q: Derive the Lorentz transformation connecting a frame S (the lab frame) to a frame S′ that moves with…
A: he Lorentz transformation connecting a frame S (the lab frame) to a frame S′ that moves with respect…
Q: Quite apart from effects due to Earth’s rotational and orbital motions, a laboratory reference frame…
A: Given:- L = 20cm = 0.2m v = 0.992c = 0.992 x 3 x 108 m/s = 2.976 x 108 m/s
Q: in a particular inertial frame S, two events occur a distance of 1.0 km apart with event 1 occuring…
A: Answer : Consider there are two frames : S (x,y,z,t) frame and S' (x',y',z',t') frame. S' frame…
Q: Use the Lorentz transformation to derive the expression for length contraction. Note that the length…
A:
Q: (u1, u, u) in S'. Prove from the Q.10 A particle has velocity u velocity transformation foumulae…
A:
Q: Give the transformation laws for the following tensors: (a) T" (b) ÔA“ / Ə2; (1 skalar/scalar); (c)…
A:
Q: Frame {2} is rotated with respect to frame {1} about the x-axis by an angle of 45°. The position of…
A: Given: |P2 = [7.0 5.0 7.0] 2A= [2.0 4.0 6.0]
Q: Starting from the Lorentz transformation, derive time dilation, Please please sketch the situation…
A: To derive , The time dilation from Lorentz transformation Consider two frames S and S' such that…
Q: Obtain the expression for the generalised momentum for the relativistic particle when the Kangra…
A: The Lagrangian of the particle is given as, L=-mc2γ-U. TO DETERMINE: The generalized momentum for…
Q: Consider the point of view of an observer who is moving toward the Earth at the same velocity as the…
A: As per the theory of relativity when an object is moving its length is measured to be shorter than…
Q: Starting from the Lorentz transformation, derive time dilation ?t = ? ?t0. Sketch the situation,…
A:
Q: Observations of the redshift of light emitted by a quasar Q1 indicate that it is moving away from…
A: We are given velocity of quasar Q1. We are also given the velocity of quasar Q2 also. We have to…
Q: A right angled triangle has two equal sides of length 22 m meters each that are placed on the x and…
A: Given data, Length of each equal side of the triangle = 22 m Speed of the moving frame = 0.61C…
Q: Find the speed of a GPS satellite (height is 20,200 km above the surface of Earth). Hence find the…
A: By using equation, v = ( G m2 / R + h )1/2 v= ( 6.67 x 10-11 x 5.98 x1024 / 20200 x 103 + 6.38 x 106…
Q: An observer standing by the railroad tracks observes two bolts of lightning strike the ends of a…
A: The length of the train, L = 300 m (measured from the reference frame)The middle of the train…
Q: A particle moves with a velocity p' in the x'y' plane of the rocket frame in a direction that makes…
A: vx = the velocity component in the laboratory frame along the x-axis, vx' = the velocity component…
Q: 5. Consider now the transformation Q=-p, P = q + Ap². a) Is this transformation canonical?
A:
Q: Events A and B occur simultaneously in an inertial frame Z and 150,000 km apart on its x-axis. Find…
A: Solution: Given that the events A and B occur simultaneously in an inertial frame Z and its spatial…
Q: Bob and Cathy are in spaceships that pass by each other. Bob gives space and time B-coordinates and…
A: Given: B coordinate = P · C coordinatetx=αββαt'x'
Q: Consider the transformation given by the Cartesion framework. L = [1 A] A: 3x3 matrix Show that A is…
A: It is given that,transformation cartesian frameworkL=100AWhere, A→3×3 matrix. Now we have to show L…
Q: 1.5 45° The objective of this question is to determine the position of the point P; relative to the…
A: Given : there is two frame position of origin of frame b relative to frame a on x is = 4 position…
Q: Problem 36.b Starting from the Lorentz transformation, derive time dilation At = y Ato. Sketch the…
A: Consider 2 successive events occuring at the same point x' in the inertial frame s'.Let t1' and t2'…
Q: Please derive a' (acceleration vector) in general Lorentz coordinates and discuss transformation law…
A: coordinate acceleration {\displaystyle \mathbf {a} =\left(a_{x},\ a_{y},\ a_{z}\right)} is the first…
Please derive the attatched velocity transformations by using the Lorentz transformation for the velocity four vector (uμ). (hint: two of the Lorentz transformation equations are needed to solve this)
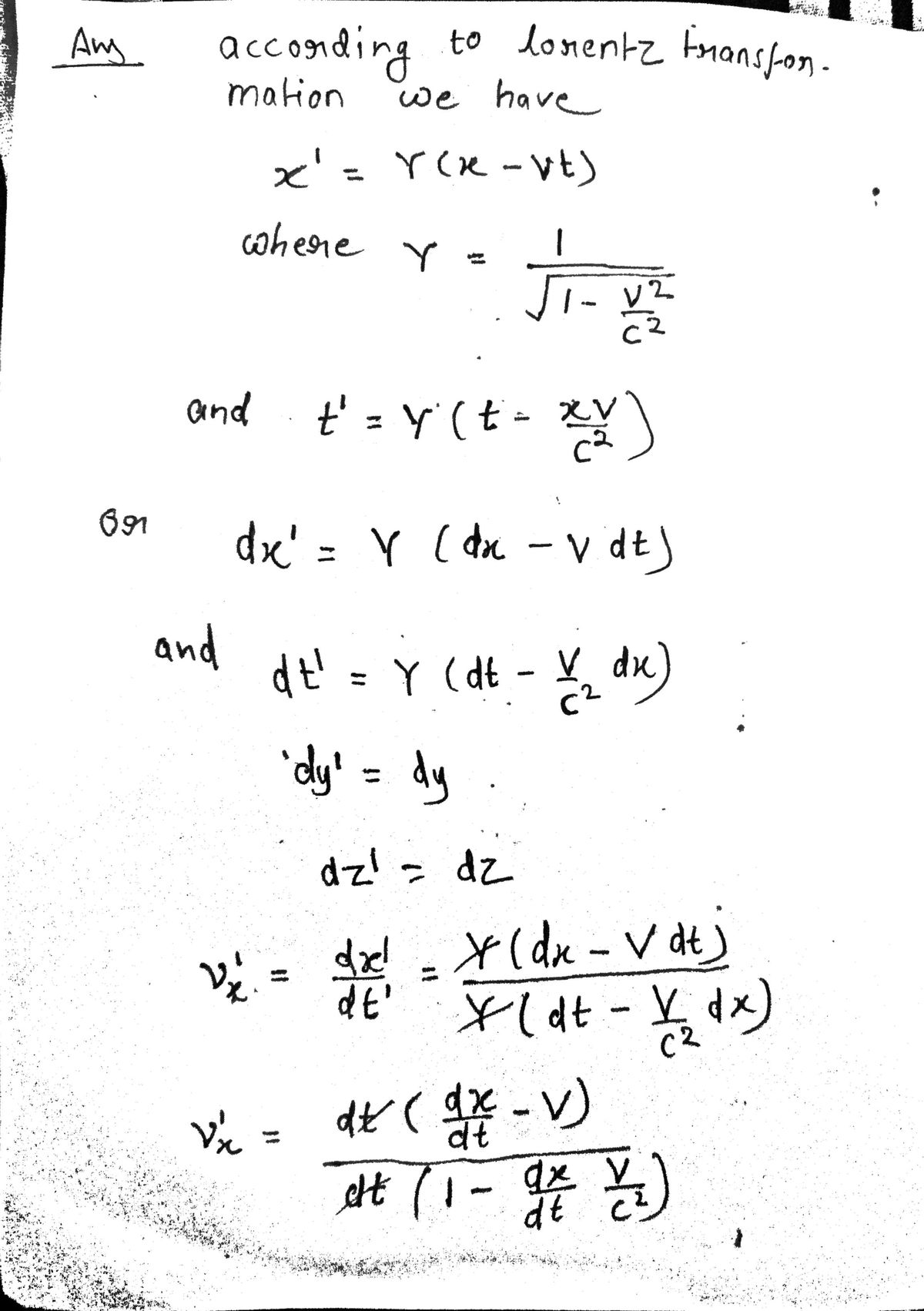
Step by step
Solved in 2 steps with 2 images
