Please answer this in a written format so that it is readable! Thank you! The average number of red blood cells per cubic mm in humans is about 5 million. We'll let μ = 5,000,000, and σ = 500,000. Let's also assume that the number of red blood cells follows a normal distribution. a) Give the values for the number of red blood cells for the middle 80% of people. (Hint/comment: if, for example, you want values for the middle 50%, you need to figure out many percent go in each tail. Note also that you will need two numbers in your answer. Draw a picture to help you.) b) Give the values for the number of red blood cells for the middle 98% of people. c) Give the 99th percentile. d) Are you surprised by the answers to (b) and (c)? Explain. If you're not sure what's going on, draw some pictures of the normal curves. e) Calculate the 1st percentile
Please answer this in a written format so that it is readable! Thank you!
The average number of red blood cells per cubic mm in humans is about 5 million. We'll let μ = 5,000,000, and σ = 500,000. Let's also assume that the number of red blood cells follows a
a) Give the values for the number of red blood cells for the middle 80% of people. (Hint/comment: if, for example, you want values for the middle 50%, you need to figure out many percent go in each tail. Note also that you will need two numbers in your answer. Draw a picture to help you.)
b) Give the values for the number of red blood cells for the middle 98% of people.
c) Give the 99th percentile.
d) Are you surprised by the answers to (b) and (c)? Explain. If you're not sure what's going on, draw some pictures of the normal curves.
e) Calculate the 1st percentile.
given the mean and standard deviation for the number of red blood cells in humans as
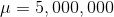
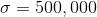
the z score for a normal distribution is given by
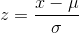
a. for middle 80% or 0.8 probability , we determine the z values corresponding to a left tail area of ,
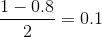
and right tail area of 0.1 . using z table we determine the corresponding z score ,

we get that
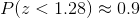
so for middle 80% the corresponding z score are -1.28 and 1.28 .
we get the number of blood cells as
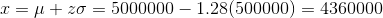
and
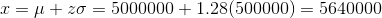
so the middle 80% of people have red blood cells from 4360000 to 5640000
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 19 images









