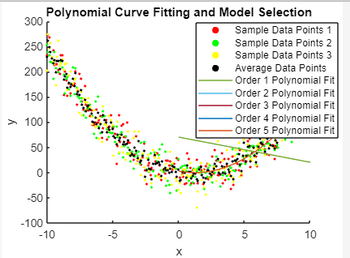
close all; clear all; clc; current_script = mfilename('fullpath'); script_directory = fileparts(current_script); file_name0 = 'data_00.csv'; file_name1 = 'data_01.csv'; file_name2 = 'data_02.csv'; file_name3 = 'data_03.csv'; data0 = csvread([script_directory '\' file_name0]); data1 = csvread([script_directory '\' file_name1]); data2 = csvread([script_directory '\' file_name2]); data3 = csvread([script_directory '\' file_name3]); avg_data = (data1 + data2 + data3) / 3; figure; % plot (data0(:,1), data0(:,2), 'b-', 'LineWidth', 2, 'DisplayName', 'Parabolic Curve'); hold on; % plot(avg_data(:, 1), avg_data(:, 2), 'k-', 'Linewidth', 1, 'DisplayName', 'Average Data Points'); plot(smooth_data(:, 1), smooth_data(:, 2), 'k-', 'Linewidth', 1, 'DisplayName', 'Smoothed Data'); scatter(data1(:,1), data1(:,2), 5, 'r', 'filled', 'DisplayName', 'Sample Data Points 1'); scatter(data2(:,1), data2(:,2), 5, 'g', 'filled', 'DisplayName', 'Sample Data Points 2'); scatter(data3(:,1), data3(:,2), 5, 'y', 'filled', 'DisplayName', 'Sample Data Points 3'); scatter(avg_data(:,1), avg_data(:,2), 5, 'k', 'filled', 'DisplayName', 'Average Data Points'); title('Parabolic Function with Noisy Data Points'); xlabel('x'); ylabel('y'); legend('Location', 'North'); grid on; hold off; - Correct for my errors - Implement in MATLAB the algorithms for: Lagrange Interpolating Polynomial (LIP) - For polynomial curve fitting, examine 1st to 5th polynomial order then determine the right order to be used using the least value of AIC (Akaike Information Criterion) and BIC (Bayesian Information Criterion). Discuss the concepts and discuss the differences between AIC and BIC. - For the final evaluation of your curve fitting functions, use the Root Mean Square Error and Mean Absolute Error as the final metrics against Data 00. - Include plots/graphs.

Database System Concepts

7th Edition

ISBN:9780078022159

Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan

Publisher:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan

Chapter1: Introduction

Section: Chapter Questions

Problem 1PE

See similar textbooks

Related questions

Question

close all;
clear all;
clc;

current_script = mfilename('fullpath');
script_directory = fileparts(current_script);

file_name0 = 'data_00.csv';
file_name1 = 'data_01.csv';
file_name2 = 'data_02.csv';
file_name3 = 'data_03.csv';

data0 = csvread([script_directory '\' file_name0]);
data1 = csvread([script_directory '\' file_name1]);
data2 = csvread([script_directory '\' file_name2]);
data3 = csvread([script_directory '\' file_name3]);

avg_data = (data1 + data2 + data3) / 3;

figure;
% plot (data0(:,1), data0(:,2), 'b-', 'LineWidth', 2, 'DisplayName', 'Parabolic Curve');

hold on;
% plot(avg_data(:, 1), avg_data(:, 2), 'k-', 'Linewidth', 1, 'DisplayName', 'Average Data Points');
plot(smooth_data(:, 1), smooth_data(:, 2), 'k-', 'Linewidth', 1, 'DisplayName', 'Smoothed Data');

scatter(data1(:,1), data1(:,2), 5, 'r', 'filled', 'DisplayName', 'Sample Data Points 1');
scatter(data2(:,1), data2(:,2), 5, 'g', 'filled', 'DisplayName', 'Sample Data Points 2');
scatter(data3(:,1), data3(:,2), 5, 'y', 'filled', 'DisplayName', 'Sample Data Points 3');
scatter(avg_data(:,1), avg_data(:,2), 5, 'k', 'filled', 'DisplayName', 'Average Data Points');
title('Parabolic Function with Noisy Data Points'); xlabel('x'); ylabel('y'); legend('Location', 'North');
grid on;
hold off;

- Correct for my errors
- Implement in MATLAB the algorithms for: Lagrange Interpolating Polynomial (LIP)
- For polynomial curve fitting, examine 1st to 5th polynomial order then determine the right order to be used using the least value of AIC (Akaike Information Criterion) and BIC (Bayesian Information Criterion). Discuss the concepts and discuss the differences between AIC and BIC.
- For the final evaluation of your curve fitting functions, use the Root Mean Square Error and Mean Absolute Error as the final metrics against Data 00.
- Include plots/graphs.

Expert Solution

Step by step

Solved in 5 steps with 9 images

SEE SOLUTION Check out a sample Q&A here

Follow-up Questions

Read through expert solutions to related follow-up questions below.

Follow-up Question

What if the data given gives a parabolic curve function? How to fix the linear line? Pls give me the correct code.

300
250
200
150
> 100
50
0
-50
-100
Polynomial Curve Fitting and Model Selection
Sample Data Points 1
Sample Data Points 2
Sample Data Points 3
Average Data Points
Order 1 Polynomial Fit
Order 2 Polynomial Fit
Order 3 Polynomial Fit
Order 4 Polynomial Fit
- Order 5 Polynomial Fit
-10
0
X
5
10

Solution

by Bartleby Expert

SEE SOLUTION

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.

Similar questions