The following figures represent the number of positive signals of water availability from an under exploration location for twenty different tests. 20 14 21 29 43 17 15 26 8 14 39 23 16 46 28 11 26 35 26 28 Using a 5% significance level, test the hypothesis that the mean of the positive signals is more than 20.Using a 5% significance level, test the hypothesis that the mean of the positive signals is different from 20.

Answered: owing figures represent the number of…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Question

The following figures represent the number of positive signals of water availability from an under exploration location for twenty different tests.

20 14 21 29 43 17 15 26 8 14

39 23 16 46 28 11 26 35 26 28

Using a 5% significance level, test the hypothesis that the mean of the positive signals is more than 20.
Using a 5% significance level, test the hypothesis that the mean of the positive signals is different from 20.

Definition Definition Measure of central tendency that is the average of a given data set. The mean value is evaluated as the quotient of the sum of all observations by the sample size. The mean, in contrast to a median, is affected by extreme values. Very large or very small values can distract the mean from the center of the data. Arithmetic mean: The most common type of mean is the arithmetic mean. It is evaluated using the formula: μ = 1 N ∑ i = 1 N x i Other types of means are the geometric mean, logarithmic mean, and harmonic mean. Geometric mean: The nth root of the product of n observations from a data set is defined as the geometric mean of the set: G = x 1 x 2 ... x n n Logarithmic mean: The difference of the natural logarithms of the two numbers, divided by the difference between the numbers is the logarithmic mean of the two numbers. The logarithmic mean is used particularly in heat transfer and mass transfer. ln x 2 − ln x 1 x 2 − x 1 Harmonic mean: The inverse of the arithmetic mean of the inverses of all the numbers in a data set is the harmonic mean of the data. 1 1 x 1 + 1 x 2 + ...

Expert Solution

Step 1

a).

The raw data is given to us. Hence, first we need to find the Mean and Standard deviation of this sample. I will use EXCEL to obtain mean and standard deviation.

Use the formula "=AVERAGE( Range of data set)" in Excel to obtain the mean of the sample. The answer obtained is 24.25
Use the formula "=STDEV.S( Range of data set)" in Excel to obtain the standard deviation of the sample. The answer obtained is 10.5225.

The snips are as follows;

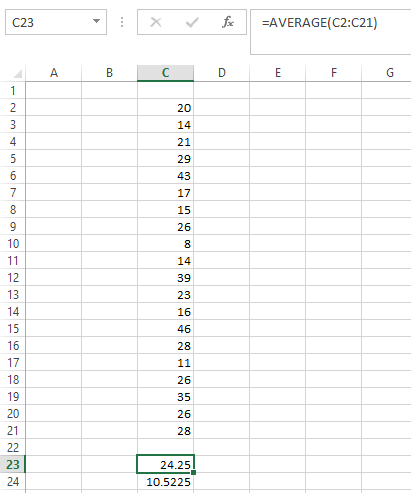
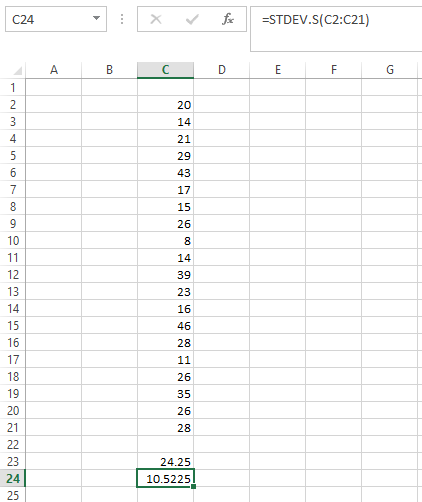
Hence, now we have

$\bar{x} = s a m p l e m e a n = 24.25 s = s a m p l e s \tan d a r d d e v i t a i o n = 10.5225 μ = p o p u l a t i o n m e a n = 20 n = s a m p l e s i z e = 20$

The null hypothesis states that mean is equal to 20, whereas the alternative hypothesis states that mean is greater than 20. Symbolically it is represented as,

$H_{0} : μ = 20 H_{a} : μ > 20$

Hence, we see that it is right tailed test.

NOTE: As the population standard deviation is not provided, we will use the t-test, because t-test is executed when the population standard deviation is unknown.

The formula and calculations for the t-test statistic is as follows;

$t = \frac{\bar{x} - μ}{\frac{s}{\sqrt{n}}} = \frac{24.25 - 20}{\frac{10.5225}{\sqrt{20}}} = 1.8062 \approx 1.81$

Now, we need to calculate the degrees of freedom. It is calculated as;

df=n-1=20-1=19

We have significance level, i.e, $α = 5 % = 0.05$

Now, we need to obtain the p-value. Observe t=1.81 and df=19 in the t-statistical table to obtain the p-value.
For left tailed, The answer obtained is 0.0431.

The decision rule states that if the p-value is less than the significance level, then we reject the null hypothesis.

In this case, 0.0431<0.05, hence we Reject the null hypothesis.
It is then concluded that the mean of the positive signals is more than 20.