|A|² 2000 ei (p-p')x/hdx = |A|² 2л hd(p - p').
Related questions
Question
100%
Hi! Could you please explain why exponential function became Dirac delta function in 3.31 (marked by green lines )

Transcribed Image Text:Example 3.2
Find the eigenfunctions and eigenvalues of the momentum operator (on the interval - 0<x<∞
).
Solution: Let fp(x) be the eigenfunction and p the eigenvalue:
d
-ih fp(x) = pfp(x).
dx
The general solution is
fp (x) = Aeipx/h
This is not square-integrable for any (complex) value of p—the momentum operator has no
eigenfunctions in Hilbert space.
And yet, if we restrict ourselves to real eigenvalues, we do recover a kind of ersatz
"orthonormality." Referring to Problems 2.23(a) and 2.26,
f (x) fp(x)dx = \AP² [¹(p-p')x/hdx = \A\² 2π hô(p − p').
88
If we pick A = 1/√2h, so that
fp(x) =
1
e/px/h
(3.30)
3-
(3.31)
(3.32)
Expert Solution
Step 1
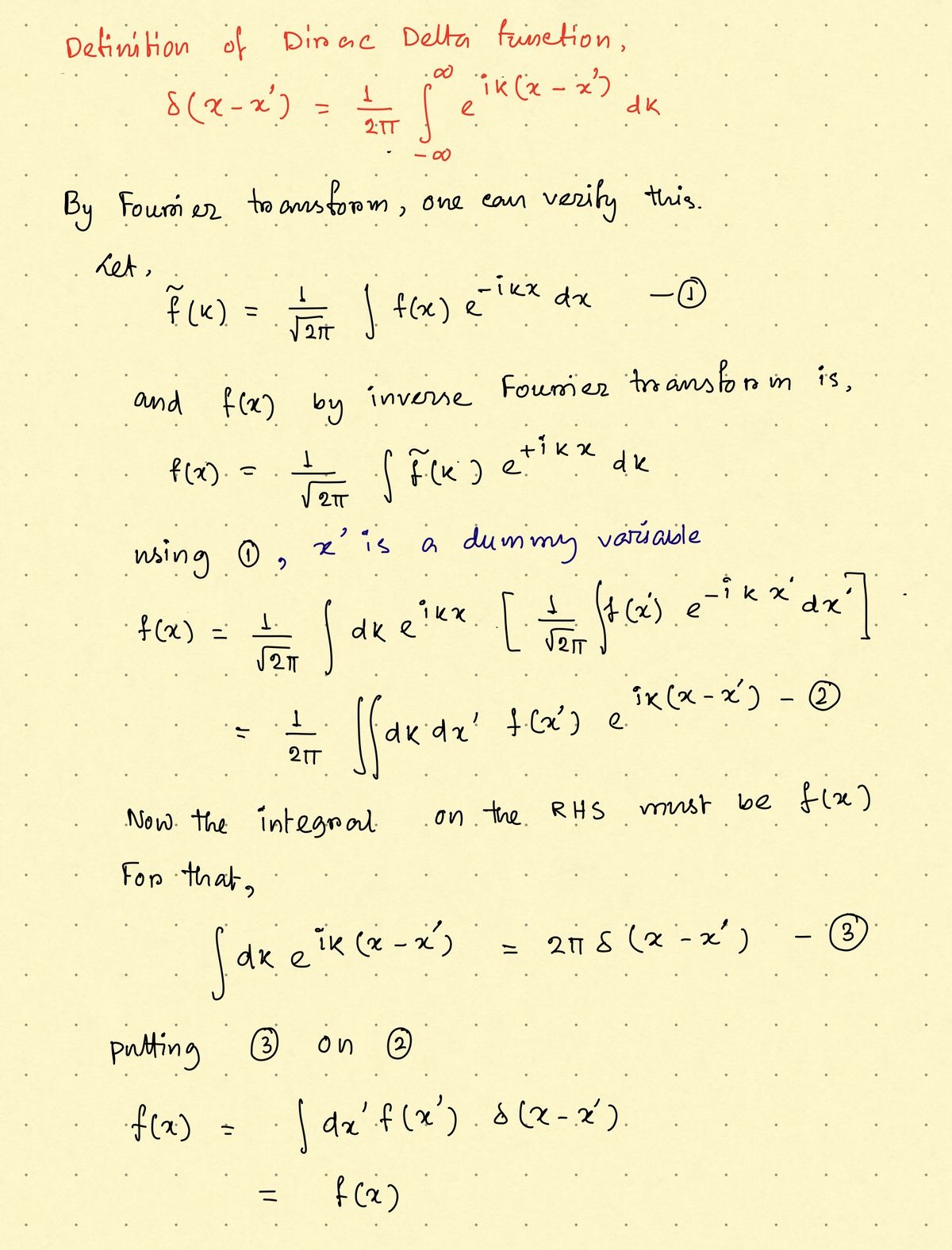
Step by step
Solved in 2 steps with 2 images
