One end of a string is secured to the ceiling of a classroom, and the other end of the string is attached to a sphere of mass 0.2 kg. The sphere is raised at an angle of 15o above the sphere’s equilibrium position and then released from rest so that the pendulum oscillates, as shown in the figure. Location 1 is shown in the figure. A graph of the pendulum’s horizontal position as a function of time is shown in the graph. Calculate the maximum kinetic energy of the sphere as it oscillates.
One end of a string is secured to the ceiling of a classroom, and the other end of the string is attached to a sphere of mass 0.2 kg. The sphere is raised at an angle of 15o above the sphere’s equilibrium position and then released from rest so that the pendulum oscillates, as shown in the figure. Location 1 is shown in the figure. A graph of the pendulum’s horizontal position as a function of time is shown in the graph.
Calculate the maximum kinetic energy of the sphere as it oscillates.

Given data:
- The mass of the sphere is .
- The angle is .
Let, L is the length of the string.
The schematic diagram can be drawn as:
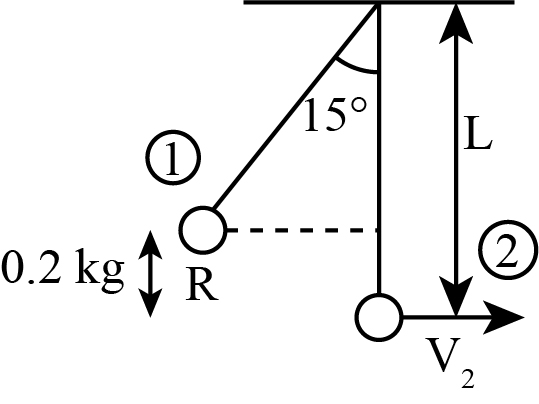
From the figure, the expression for the distance R can be written as:
Now apply the conservation of energy principle as:
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images
