ofs (portfolio). Let an be a sequence decreasing to zero. Prove that En-1(-1)"an converges.
ofs (portfolio). Let an be a sequence decreasing to zero. Prove that En-1(-1)"an converges.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Need help with Task 4, this is a homework question not an exam.
![**Real Analysis - Homework Number 4**
*Due: September 20, 2023*
---
**Meta Tasks**
*Sorry this one is late, take until Monday if you want.*
**Task 1.** Prove that the sequence \( a_n \) converges. The sequence is defined by \( a_0 = \sqrt{2} \) and \( a_n = \sqrt{2 + a_{n-1}} \).
**Task 2.** Let \( a_n \) be a sequence such that every open interval containing 3 has infinitely many points from the sequence. Similarly, every open interval containing \(-2\) has infinitely many points from the sequence. For every \( x \neq -2, 3 \) there exists an open interval around \( x \) such that the interval only contains finitely many points from the sequence.
Say as much as you can about this sequence.
**Task 3.** Prove, including all relevant details, what interval the following series converges absolutely on. Check what happens at the endpoints.
\[
\sum_{n=1}^{\infty} \frac{(x-3)^n}{2n(n-1)}
\]
---
**Proofs**
**Task 4** (portfolio). Let \( a_n \) be a sequence decreasing to zero. Prove that \( \sum_{n=1}^{\infty} (-1)^n a_n \) converges.
**Task 5.** Let \( a_n \) be a positive sequence that decreases to zero. Set
\[
S_N = \sum_{n=1}^{N} a_n.
\]
Is \(\limsup S_N\) necessarily finite? Provide either a proof that it is or a counterexample that it isn’t always.
**Task 6.** Prove Proposition 1.3.10.
*Note: Handwritten note on the paper: "Every open interval has \(-2\) and 3".*
---](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F47675d24-ba7f-4e21-93eb-97faaaed8f8d%2F2ac0af1d-c537-46df-a72b-077de1aaaac4%2Fdf3qx4_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Real Analysis - Homework Number 4**
*Due: September 20, 2023*
---
**Meta Tasks**
*Sorry this one is late, take until Monday if you want.*
**Task 1.** Prove that the sequence \( a_n \) converges. The sequence is defined by \( a_0 = \sqrt{2} \) and \( a_n = \sqrt{2 + a_{n-1}} \).
**Task 2.** Let \( a_n \) be a sequence such that every open interval containing 3 has infinitely many points from the sequence. Similarly, every open interval containing \(-2\) has infinitely many points from the sequence. For every \( x \neq -2, 3 \) there exists an open interval around \( x \) such that the interval only contains finitely many points from the sequence.
Say as much as you can about this sequence.
**Task 3.** Prove, including all relevant details, what interval the following series converges absolutely on. Check what happens at the endpoints.
\[
\sum_{n=1}^{\infty} \frac{(x-3)^n}{2n(n-1)}
\]
---
**Proofs**
**Task 4** (portfolio). Let \( a_n \) be a sequence decreasing to zero. Prove that \( \sum_{n=1}^{\infty} (-1)^n a_n \) converges.
**Task 5.** Let \( a_n \) be a positive sequence that decreases to zero. Set
\[
S_N = \sum_{n=1}^{N} a_n.
\]
Is \(\limsup S_N\) necessarily finite? Provide either a proof that it is or a counterexample that it isn’t always.
**Task 6.** Prove Proposition 1.3.10.
*Note: Handwritten note on the paper: "Every open interval has \(-2\) and 3".*
---
Expert Solution
Step 1: Given information
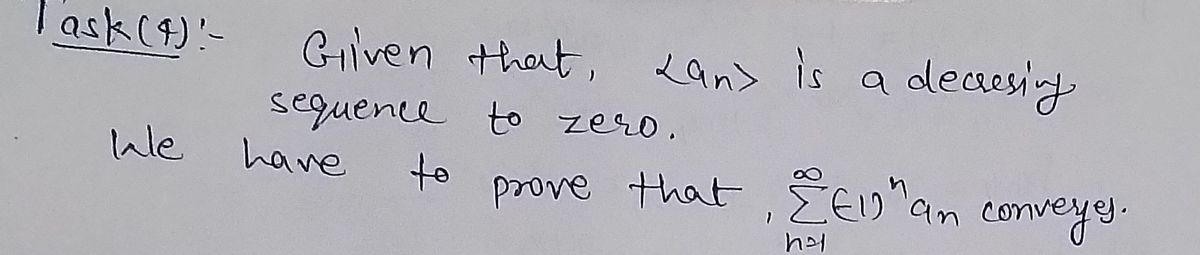
Step by step
Solved in 3 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

