ƒ:R\{}} → R defined by f(x) = x² 5x-9 is continuous at xo = 2.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
See the attachment. Please answer the question with all processes and detailed explanation. And please meet the requirements.

Transcribed Image Text:2. Prove, using the ε-8 definition of continuity that the function
x²
5x-9
ƒ : R\{}} → R defined by ƒ(x) =
=
is continuous at xo
=
2.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 3 steps with 3 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Is this a mistake? Because the middle term in the inequality is 5 epsilon times a number which is bigger than 1. Then 5 epsilon should be smaller. And I don't really understand the inequality in step 3, for example, if we let x=17, then the numerator will be positive while we get a negative denominator. The result will be negative, that is smaller than 1.
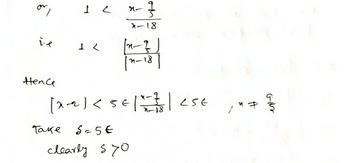
Transcribed Image Text:Hence
ㅗㄴ
take
r<
3
x-18
121-
11-18
[21C5티올옮lese
56
-18
S-56
clearly syo
+
6
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

