Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
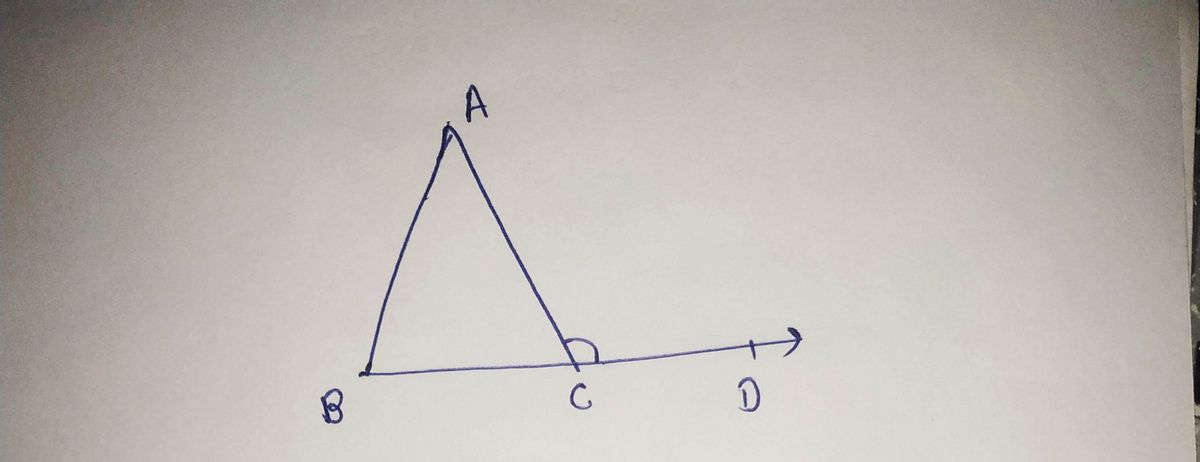
Now, suppose we decide to work in Hyperbolic Geometry. What do we know about angle ACD elative to the angles at A and B, e.g., what can be said about an exterior angle relative to its pposite interior angles? How do you know so? (In other words, informally justify your claim.) Let AABC be given, and suppose D is a point on BC such that B - C - D. Then ZACD is called an exterior angle of the given triangle. The angles at A and B of AABC are called opposite interior angles of ZACD. ( EXTERIOR ANGLE OF A TRIANGLE Figure 3.27 D

Now, suppose we decide to work in Hyperbolic Geometry. What do we know about angle ACD elative to the angles at A and B, e.g., what can be said about an exterior angle relative to its pposite interior angles? How do you know so? (In other words, informally justify your claim.) Let AABC be given, and suppose D is a point on BC such that B - C - D. Then ZACD is called an exterior angle of the given triangle. The angles at A and B of AABC are called opposite interior angles of ZACD. ( EXTERIOR ANGLE OF A TRIANGLE Figure 3.27 D

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question
Now, suppose we decide to work in Hyperbolic Geometry. What do we know about angle ACD relative to the angles at A and B, e.g., what can be said about an exterior angle relative to its opposite interior angles? How do you know so? (In other words, informally justify your claim.) Let AABC be given, and suppose D is a point on BC such that B - C - D. Then ZACD is called an exterior angle of the given triangle. The angles at A and B of AABC are called opposite interior angles of ZACD. ( EXTERIOR ANGLE OF A TRIANGLE Figure 3.27
Transcribed Image Text:Now, suppose we decide to work in Hyperbolic Geometry. What do we know about angle ACD relative to the angles at A and B, e.g., what can be said about an exterior angle relative to its opposite interior angles? How do you know so? (In other words, informally justify your claim.) Let AABC be given, and suppose D is a point on BC such that B - C - D. Then ZACD is called an exterior angle of the given triangle. The angles at A and B of AABC are called opposite interior angles of ZACD. ( EXTERIOR ANGLE OF A TRIANGLE Figure 3.27
Expert Solution
Step 1

Advanced Math homework question answer, step 1, image 1

trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS