Now consider f(x) = ! defined for all real numbers except for x = 0. Appealing to the e-8 definition, prove that no real number LER can be a limit of f(x) as x tends to 0, i.e., no matter what you choose for L, limz0 L. (3.1.4) Preliminary Work Wuit
Now consider f(x) = ! defined for all real numbers except for x = 0. Appealing to the e-8 definition, prove that no real number LER can be a limit of f(x) as x tends to 0, i.e., no matter what you choose for L, limz0 L. (3.1.4) Preliminary Work Wuit
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:**Preliminary Work and Exploration of Limits**
**Function Analysis:**
Consider the function \( f(x) = \frac{1}{x} \), which is defined for all real numbers except for \( x = 0 \).
**Objective:**
Prove that no real number \( L \in \mathbb{R} \) can be the limit of \( f(x) \) as \( x \) approaches 0. This is expressed formally as \( \lim_{x \to 0} \frac{1}{x} \neq L \).
**Preliminary Work (3.1.4):**
- Write down and explore your thought process.
- Analyze how \( f(x) \) behaves as \( x \) approaches 0 from both the positive and negative sides.
- Use the \( \epsilon\)–\( \delta \) definition of a limit to support your explanation.
**Formal Proof (3.1.5):**
Prepare a structured and rigorous mathematical proof to demonstrate the claim.
Expert Solution
Step 1
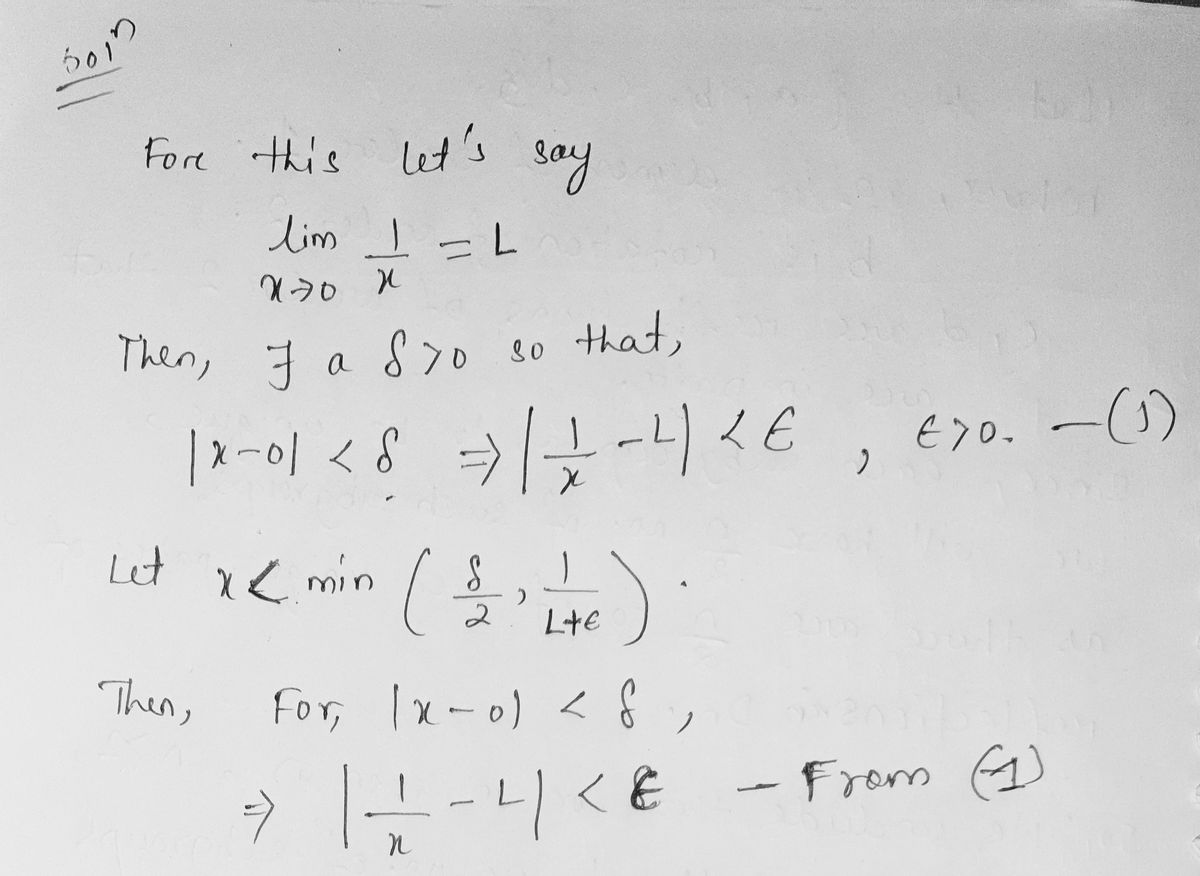
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

