College Physics
11th Edition
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Raymond A. Serway, Chris Vuille
Chapter1: Units, Trigonometry. And Vectors
Section: Chapter Questions
Problem 1CQ: Estimate the order of magnitude of the length, in meters, of each of the following; (a) a mouse, (b)...
Related questions
Question
100%
I need help, some explanation would be much appreciated for upcoming homework. Thanks in advance.
![**Problem 3: A Golf Ball**
A golf ball is hit from the top of a 60 m tall building, and the position of the ball as a function of time is given by:
\[
\vec{r}(m) = (20.0 \cdot t) \hat{i} + (60 + 30.0 \cdot t - 5.0 \cdot t^2) \hat{j}
\]
a. Indicate the units and physical meaning of each coefficient.
b. Determine the initial velocity of the golf ball.
c. How long does it take the ball to hit the ground?
---
**Explanation:**
- The equation for the position of the golf ball is given in vector form, where \( \hat{i} \) and \( \hat{j} \) denote horizontal and vertical components respectively.
- In the equation:
- \(20.0 \cdot t\) represents horizontal motion with a constant velocity coefficient of 20.0 \( \frac{m}{s} \).
- \(60 + 30.0 \cdot t - 5.0 \cdot t^2\) represents vertical motion with:
- An initial height of 60 meters.
- An initial vertical velocity component coefficient of 30.0 \( \frac{m}{s} \).
- A downward acceleration due to gravity represented by \( -5.0 \cdot t^2 \), assuming gravity is \(10 \frac{m}{s^2} \) and divided by 2 in the kinematic equation.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fb40a18ca-f6bf-46d9-9516-d1f637f7b776%2Fb70400a5-637e-40ed-a399-9f26f014b233%2Faftl84_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem 3: A Golf Ball**
A golf ball is hit from the top of a 60 m tall building, and the position of the ball as a function of time is given by:
\[
\vec{r}(m) = (20.0 \cdot t) \hat{i} + (60 + 30.0 \cdot t - 5.0 \cdot t^2) \hat{j}
\]
a. Indicate the units and physical meaning of each coefficient.
b. Determine the initial velocity of the golf ball.
c. How long does it take the ball to hit the ground?
---
**Explanation:**
- The equation for the position of the golf ball is given in vector form, where \( \hat{i} \) and \( \hat{j} \) denote horizontal and vertical components respectively.
- In the equation:
- \(20.0 \cdot t\) represents horizontal motion with a constant velocity coefficient of 20.0 \( \frac{m}{s} \).
- \(60 + 30.0 \cdot t - 5.0 \cdot t^2\) represents vertical motion with:
- An initial height of 60 meters.
- An initial vertical velocity component coefficient of 30.0 \( \frac{m}{s} \).
- A downward acceleration due to gravity represented by \( -5.0 \cdot t^2 \), assuming gravity is \(10 \frac{m}{s^2} \) and divided by 2 in the kinematic equation.

Transcribed Image Text:Certainly! Here is the transcribed text for an educational website:
---
**Physics Problem: Analyzing the Motion of a Golf Ball**
**d. Calculate the range of the golf ball.**
**e. Determine the final velocity of the golf ball.**
---
In this exercise, students are tasked with calculating the range and final velocity of a golf ball. These tasks are typical in physics problems related to projectile motion, where you analyze the horizontal distance traveled by the ball (range) and the speed at which it moves just before hitting the ground (final velocity).
Given these types of problems, students generally apply formulas from kinematics, such as:
- **Range Formula:** \( R = \frac{v_i^2 \sin(2\theta)}{g} \)
- **Final Velocity Formula:** Incorporating both horizontal and vertical components using vector addition.
Where:
- \( R \) is the range,
- \( v_i \) is the initial velocity of the ball,
- \( \theta \) is the launch angle,
- \( g \) is the acceleration due to gravity.
Understanding these concepts helps in analyzing motion across different fields, not just sports.
Expert Solution
Step 1
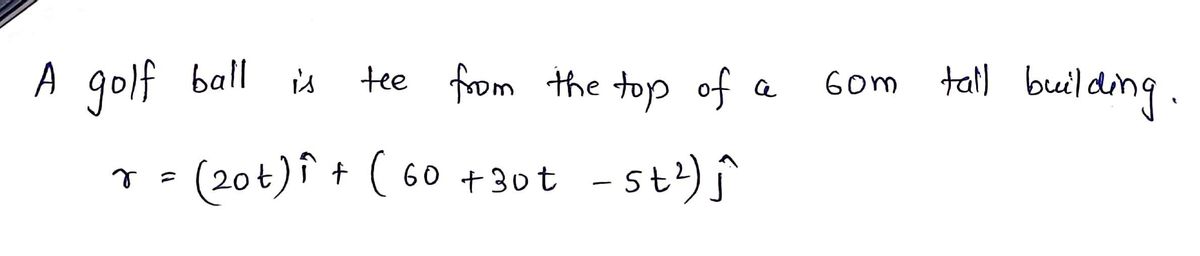
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Only parts D and E. ( i did not know about the first3 parts in the guidelines)
![**Problem 3: A golf ball.**
A golf ball is thrown from the top of a 60 m tall building. The position of the ball as a function of time is given by:
\[
\vec{r}(m) = (20.0 \cdot t)\hat{i} + (60 + 30.0 \cdot t - 5.0 \cdot t^2)\hat{j}
\]
a. Indicate the units and physical meaning of each coefficient.
b. Determine the initial velocity of the golf ball.
c. How long does it take the ball to hit the ground?](https://content.bartleby.com/qna-images/question/b40a18ca-f6bf-46d9-9516-d1f637f7b776/582fe44c-ce07-4e7f-98c3-f512d21ce7df/vnaazn_thumbnail.jpeg)
Transcribed Image Text:**Problem 3: A golf ball.**
A golf ball is thrown from the top of a 60 m tall building. The position of the ball as a function of time is given by:
\[
\vec{r}(m) = (20.0 \cdot t)\hat{i} + (60 + 30.0 \cdot t - 5.0 \cdot t^2)\hat{j}
\]
a. Indicate the units and physical meaning of each coefficient.
b. Determine the initial velocity of the golf ball.
c. How long does it take the ball to hit the ground?
![**Exercise on Projectile Motion: Golf Ball Analysis**
**d. Task: Calculate the range of the golf ball.**
In this section, students are required to compute the horizontal distance traveled by the golf ball, known as its range. The range can be determined using the projectile motion formula:
\[ \text{Range} = \frac{{v_i^2 \cdot \sin(2\theta)}}{g} \]
Where:
- \( v_i \) is the initial velocity of the golf ball
- \( \theta \) is the launch angle
- \( g \) is the acceleration due to gravity (approximately \( 9.81 \, \text{m/s}^2 \))
**e. Task: Determine the final velocity of the golf ball.**
For this task, students are asked to find the final velocity of the golf ball upon impact. The final velocity can be calculated by considering both the horizontal and vertical components of the motion:
1. **Horizontal Component (\( v_x \))**: Remains constant throughout the motion.
2. **Vertical Component (\( v_y \))**: Can be found using the equation:
\[ v_y = v_i \cdot \sin(\theta) - g \cdot t \]
Where:
- \( t \) is the time of flight
**Final Velocity (\( v_f \))** is determined using the Pythagorean theorem:
\[ v_f = \sqrt{v_x^2 + v_y^2} \]
This analysis allows you to integrate concepts of physics such as vectors and trigonometry to solve real-world problems.](https://content.bartleby.com/qna-images/question/b40a18ca-f6bf-46d9-9516-d1f637f7b776/582fe44c-ce07-4e7f-98c3-f512d21ce7df/jqqn7ti_thumbnail.jpeg)
Transcribed Image Text:**Exercise on Projectile Motion: Golf Ball Analysis**
**d. Task: Calculate the range of the golf ball.**
In this section, students are required to compute the horizontal distance traveled by the golf ball, known as its range. The range can be determined using the projectile motion formula:
\[ \text{Range} = \frac{{v_i^2 \cdot \sin(2\theta)}}{g} \]
Where:
- \( v_i \) is the initial velocity of the golf ball
- \( \theta \) is the launch angle
- \( g \) is the acceleration due to gravity (approximately \( 9.81 \, \text{m/s}^2 \))
**e. Task: Determine the final velocity of the golf ball.**
For this task, students are asked to find the final velocity of the golf ball upon impact. The final velocity can be calculated by considering both the horizontal and vertical components of the motion:
1. **Horizontal Component (\( v_x \))**: Remains constant throughout the motion.
2. **Vertical Component (\( v_y \))**: Can be found using the equation:
\[ v_y = v_i \cdot \sin(\theta) - g \cdot t \]
Where:
- \( t \) is the time of flight
**Final Velocity (\( v_f \))** is determined using the Pythagorean theorem:
\[ v_f = \sqrt{v_x^2 + v_y^2} \]
This analysis allows you to integrate concepts of physics such as vectors and trigonometry to solve real-world problems.
Solution
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Recommended textbooks for you

College Physics
Physics
ISBN:
9781305952300
Author:
Raymond A. Serway, Chris Vuille
Publisher:
Cengage Learning

University Physics (14th Edition)
Physics
ISBN:
9780133969290
Author:
Hugh D. Young, Roger A. Freedman
Publisher:
PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:
9781107189638
Author:
Griffiths, David J., Schroeter, Darrell F.
Publisher:
Cambridge University Press

College Physics
Physics
ISBN:
9781305952300
Author:
Raymond A. Serway, Chris Vuille
Publisher:
Cengage Learning

University Physics (14th Edition)
Physics
ISBN:
9780133969290
Author:
Hugh D. Young, Roger A. Freedman
Publisher:
PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:
9781107189638
Author:
Griffiths, David J., Schroeter, Darrell F.
Publisher:
Cambridge University Press

Physics for Scientists and Engineers
Physics
ISBN:
9781337553278
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:
9780321820464
Author:
Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:
Addison-Wesley

College Physics: A Strategic Approach (4th Editio…
Physics
ISBN:
9780134609034
Author:
Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:
PEARSON