Nasonex Treatment Analysis Nasonex is a nasal spray used to treat allergies. In clinical trials, 1671 subjects were given a placebo, and 2 of them developed upper respiratory tract infections. Another 2103 patients were treated with Nasonex and 6 of them developed upper respiratory tract infections. Assume that Nasonex has no effect on upper respiratory tract infections so that the rate of those infections also applies to Nasonex users. Using the placebo rate of 2/1671, simulate groups of 2103 subjects given the Nasonex treatment, and determine whether a result of 6 upper respiratory tract infections could easily occur. What does that suggest about Nasonex as a cause of upper respiratory tract infections?
Nasonex Treatment Analysis Nasonex is a nasal spray used to treat allergies. In clinical trials, 1671 subjects were given a placebo, and 2 of them developed upper respiratory tract infections. Another 2103 patients were treated with Nasonex and 6 of them developed upper respiratory tract infections. Assume that Nasonex has no effect on upper respiratory tract infections so that the rate of those infections also applies to Nasonex users. Using the placebo rate of 2/1671, simulate groups of 2103 subjects given the Nasonex treatment, and determine whether a result of 6 upper respiratory tract infections could easily occur. What does that suggest about Nasonex as a cause of upper respiratory tract infections?
Answers will vary. One of the possible answers is given below:
Step-by-step software procedure to generate random numbers using EXCEL is as follows:
- Open an EXCEL file.
- In cell A1, enter the formula “=RANDBETWEEN (1,2103)”.
- Clicks ‘ENTER’.
Click and hold down the mouse button to drag the lower right corner of the cell A1, pull it down the column until 1,000 cells are highlighted. Repeat the procedure 5 times.
2,103 patients were treated with Nasonex and 6 of them developed upper respiratory tract infections. Consider numbers from 1 to 6 as patients who develop upper respiratory tract infections and 7 to 1,000 represent the patients who do not develop upper respiratory tract infections.
The formula for probability of an event is as follows:
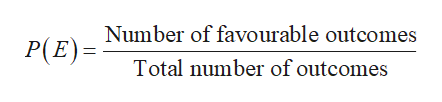
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 2 images









