Answered: My question is: Task 3. Report the…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Topic Video

Question

100%

My question is:

Task 3. Report the mean, standard deviation, skewness, and kurtosis for each of the three prior activity levels. Based on these statistics do you think the assumptions of constant variance and normality of errors are appropriate ?

Below Average (Mean = 33.42, SD - 5.477, Skewness = -1.127, Kurtosis = -0.395)

Average (Mean = 32, SD - 3.464, Skewness = 0.902, Kurtosis = -0.208)

Above Average (Mean = 24, SD - 4.427, Skewness = 1.452, Kurtosis = 1.888)

thank you

Definition Definition Measure of central tendency that is the average of a given data set. The mean value is evaluated as the quotient of the sum of all observations by the sample size. The mean, in contrast to a median, is affected by extreme values. Very large or very small values can distract the mean from the center of the data. Arithmetic mean: The most common type of mean is the arithmetic mean. It is evaluated using the formula: μ = 1 N ∑ i = 1 N x i Other types of means are the geometric mean, logarithmic mean, and harmonic mean. Geometric mean: The nth root of the product of n observations from a data set is defined as the geometric mean of the set: G = x 1 x 2 ... x n n Logarithmic mean: The difference of the natural logarithms of the two numbers, divided by the difference between the numbers is the logarithmic mean of the two numbers. The logarithmic mean is used particularly in heat transfer and mass transfer. ln x 2 − ln x 1 x 2 − x 1 Harmonic mean: The inverse of the arithmetic mean of the inverses of all the numbers in a data set is the harmonic mean of the data. 1 1 x 1 + 1 x 2 + ...

Expert Solution

Step 1

Introduction:

Mean:

Mean is an important measure of center when the data is quantitative. Mean of a data set is the sum of the data values divided by the size of the dataset.

Standard deviation:

The standard deviation is based on how much each observation deviates from a central point represented by the mean. In general, the greater the distances between the individual observations and the mean, the greater the variability of the data set.

Skewness:

The data are said to be skewed if there is lack of symmetry and values fall on one side that is, either left or right of the distribution.

Denote S_kas the coefficient of skewness.

If S_k = 0 then mean = median = mode (Symmetric distribution)

If S_k > 0 then mean > median > mode (Positive skewed distribution).

If S_k < 0 then mean < median < mode (Negative skewed distribution).

Kurtosis:

The kurtosis measures the peaked ness of the frequency curve.

Denote β₂ as the coefficient of kurtosis.

If β₂ = 3, then the curve is normal or meso-kurtic curve.

If β₂ > 3, then the curve is lepto-kurtic curve.

If β₂ < 3, then the curve is platy-kurtic curve.

Step 2

Statistical report for the methods:

Mean, standard deviation, skewness and kurtosis for each of the three prior activity levels:

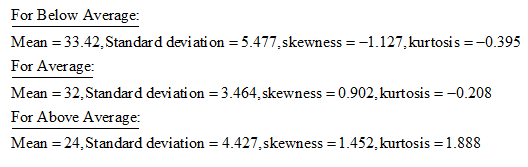
Trending now

This is a popular solution!

Step by step

Solved in 3 steps with 1 images

Knowledge Booster

$Hypothesis Tests and Confidence Intervals for Means$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Similar questions