Monthly savings in PKR DR 125000 10 85000 15 105000 28 98000 35 54000 44 800000 56 55000 68 7000 74 24000 28 0 35 Suppose that we have data on “Monthly savings in PKR” and “dependency Ratio (DR)”(percentage share of non-earners to earners, in a family). Run a regression that can help us predict the monthly savings, given the data of DR. Predict monthly savings, if DR=10, and if DR=90; interpret the results in terms of prediction accuracy
Correlation
Correlation defines a relationship between two independent variables. It tells the degree to which variables move in relation to each other. When two sets of data are related to each other, there is a correlation between them.
Linear Correlation
A correlation is used to determine the relationships between numerical and categorical variables. In other words, it is an indicator of how things are connected to one another. The correlation analysis is the study of how variables are related.
Regression Analysis
Regression analysis is a statistical method in which it estimates the relationship between a dependent variable and one or more independent variable. In simple terms dependent variable is called as outcome variable and independent variable is called as predictors. Regression analysis is one of the methods to find the trends in data. The independent variable used in Regression analysis is named Predictor variable. It offers data of an associated dependent variable regarding a particular outcome.
|
Monthly savings in PKR |
DR |
|
125000 |
10 |
|
85000 |
15 |
|
105000 |
28 |
|
98000 |
35 |
|
54000 |
44 |
|
800000 |
56 |
|
55000 |
68 |
|
7000 |
74 |
|
24000 |
28 |
|
0 |
35 |
Suppose that we have data on “Monthly savings in PKR” and “dependency Ratio (DR)”(percentage share of non-earners to earners, in a family). Run a regression that can help us predict the monthly savings, given the data of DR. Predict monthly savings, if DR=10, and if DR=90; interpret the results in terms of prediction accuracy

Data on “Monthly savings in PKR” and “dependency Ratio (DR)” (percentage share of non-earners to earners, in a family) is given as:
|
Monthly savings in PKR |
DR |
|
125000 |
10 |
|
85000 |
15 |
|
105000 |
28 |
|
98000 |
35 |
|
54000 |
44 |
|
800000 |
56 |
|
55000 |
68 |
|
7000 |
74 |
|
24000 |
28 |
|
0 |
35 |
Regression can be obtained as:
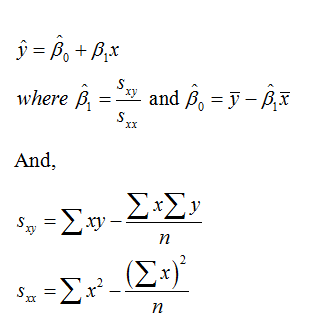
Here, Monthly savings in PKR will be dependent on dependency ratio, let y= PKR and x= DR
From provided data,
|
y |
y2 |
x |
x2 |
xy |
|
125000 |
15625000000 |
10 |
100 |
1250000 |
|
85000 |
7225000000 |
15 |
225 |
1275000 |
|
105000 |
11025000000 |
28 |
784 |
2940000 |
|
98000 |
9604000000 |
35 |
1225 |
3430000 |
|
54000 |
2916000000 |
44 |
1936 |
2376000 |
|
800000 |
640000000000 |
56 |
3136 |
44800000 |
|
55000 |
3025000000 |
68 |
4624 |
3740000 |
|
7000 |
49000000 |
74 |
5476 |
518000 |
|
24000 |
576000000 |
28 |
784 |
672000 |
|
0 |
0 |
35 |
1225 |
0 |
|
∑y= 1353000 |
∑ y2= 690045000000 |
∑x= 393 |
∑ x2= 19515 |
∑ xy= 61001000 |
y̅ = 135300
x̅= 39.3
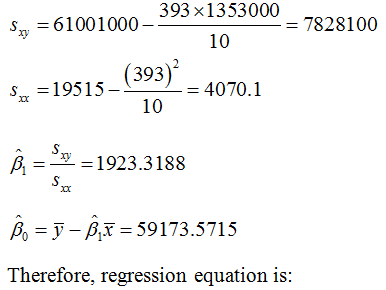
Step by step
Solved in 3 steps with 3 images









