LetPij = P(Xn+1 =jXn = i)where {Xn, n = Σ 01,2,3,...} is a Markov chain. Show that for a fixed i, j Pij = 1. =
LetPij = P(Xn+1 =jXn = i)where {Xn, n = Σ 01,2,3,...} is a Markov chain. Show that for a fixed i, j Pij = 1. =
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
100%

Transcribed Image Text:**Transcription and Explanation for Educational Website**
**Text:**
Let \( P_{ij} = P(X_{n+1} = j | X_n = i) \) where
\(\{X_n, n = 0, 1, 2, 3, \ldots\}\) is a Markov chain. Show that for a fixed \( i, \sum_j P_{ij} = 1 \).
**Explanation:**
This excerpt deals with the concept of a Markov chain, which is a sequence of random variables with a specific property: the future state depends only on the current state and not on the sequence of events that preceded it. In this context:
- \( X_n \) represents the state of the Markov chain at step \( n \).
- \( P_{ij} \) represents the probability of transitioning from state \( i \) to state \( j \) in the next step.
The statement requires us to demonstrate that for any fixed state \( i \), the sum of the transition probabilities to all possible subsequent states \( j \) is equal to 1. This reflects the fact that the process must move to some state in the next step, ensuring that probabilities are normalized. The summation across all \( j \) ensures that these probabilities cover all possible transitions from \( i \).
This property is fundamental to the definition of stochastic processes like Markov chains, emphasizing that the probability distribution over the next state is complete and sums to 1 when starting from a given current state.
Expert Solution
Step 1
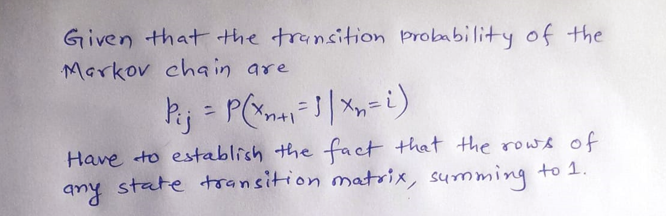
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
