Let Y (x, t = 0) = ₁/√3 + ¥₂/√4 + 3√(5/12), where ₁ is the ith normalized stationary state solution of the infinite square well. (a) Verify that Y itself is normalized (b) Find Y (x, t) and, using the explicit stationary state wavefunctions of the infinite square well, express the probability density at time t as a real function. (c) If En is the energy of the n™ normalized stationary state, what are the probabilities of measuring energy and getting the result E₁, or E2, or E3? (d) What is when written in terms of E₁ ? (e) Compute and
Let Y (x, t = 0) = ₁/√3 + ¥₂/√4 + 3√(5/12), where ₁ is the ith normalized stationary state solution of the infinite square well. (a) Verify that Y itself is normalized (b) Find Y (x, t) and, using the explicit stationary state wavefunctions of the infinite square well, express the probability density at time t as a real function. (c) If En is the energy of the n™ normalized stationary state, what are the probabilities of measuring energy and getting the result E₁, or E2, or E3? (d) What is when written in terms of E₁ ? (e) Compute and
Related questions
Question

Transcribed Image Text:Let Y (x, t = 0) = µ₁/√3 + ₂/√4 + 3√(5/12), where ¡ is the ith normalized stationary state
solution of the infinite square well.
(a) Verify that Y itself is normalized
(b) Find Y (x, t) and, using the explicit stationary state wavefunctions of the infinite square well,
express the probability density at time t as a real function.
th
(c) If En is the energy of the n™ normalized stationary state, what are the probabilities of measuring
energy and getting the result E₁, or E2, or E3?
(d) What is <H> when written in terms of E₁ ?
(e) Compute <x> and <p>
Expert Solution
Step 1: Verify wave function is normalised
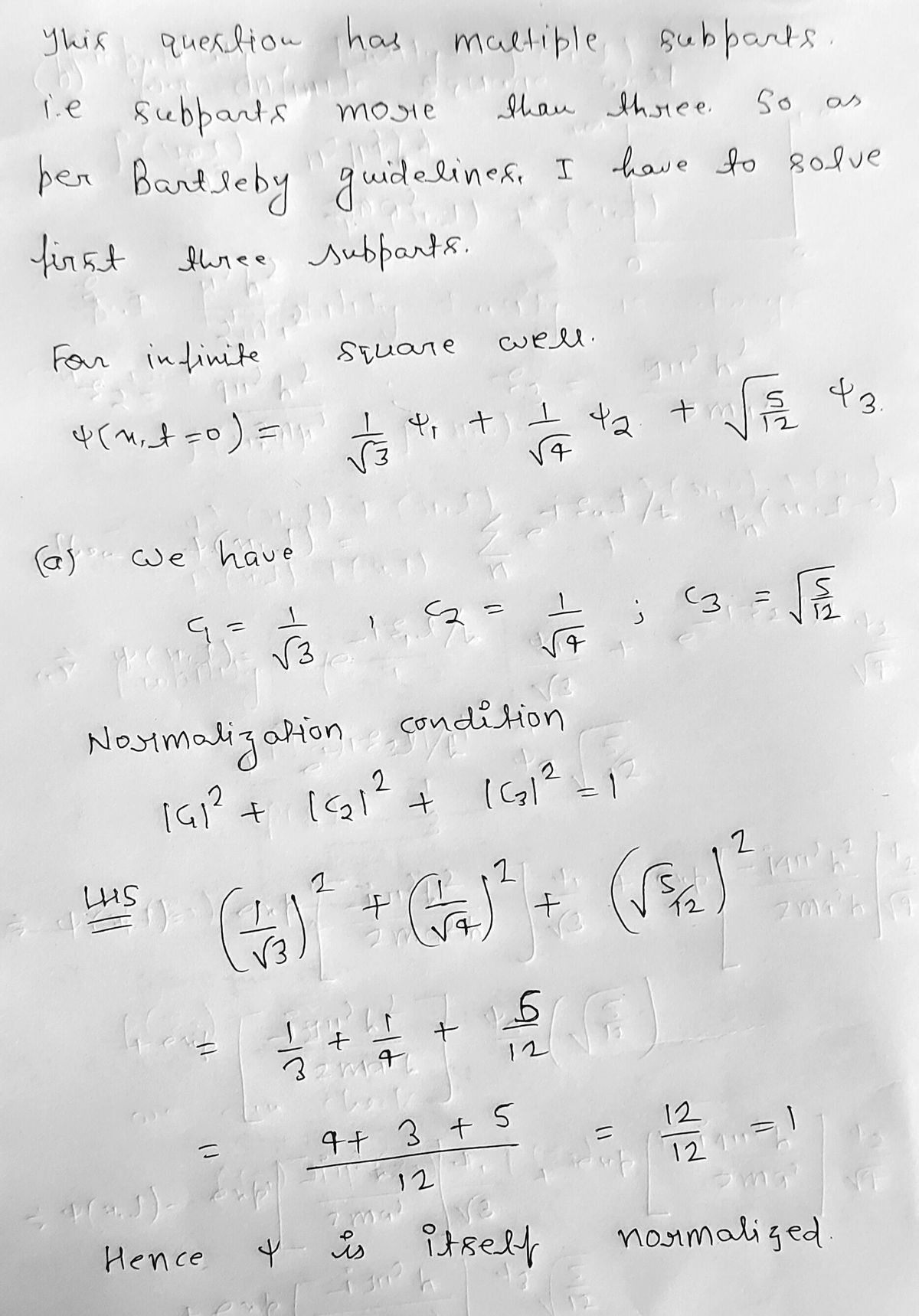
Step by step
Solved in 4 steps with 4 images
