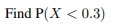Let X have pdf fx(x) = { kr(1-2), 0≤x≤1; 0, otherwise. (a) Determine the distribution function Fx (2), by firstly finding k.
Let X have pdf fx(x) = { kr(1-2), 0≤x≤1; 0, otherwise. (a) Determine the distribution function Fx (2), by firstly finding k.
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question

Transcribed Image Text:Let X have pdf
= {
(a) Determine the distribution function Fx (x), by firstly finding k.
fx
kr(1-x), 0≤x≤ 1;
otherwise.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Transcribed Image Text:(b) Use R to plot the pdf and df of X on the same graph.
Solution
Similar questions
Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON