Let x = age in years of a rural Quebec woman at the time of her first marriage. In the year 1941, the population variance of x was approximately σ2 = 5.1. Suppose a recent study of age at first marriage for a random sample of 51 women in rural Quebec gave a sample variance s2 = 2.7. Use a 5% level of significance to test the claim that the current variance is less than 5.1. Find a 90% confidence interval for the population variance.
Let x = age in years of a rural Quebec woman at the time of her first marriage. In the year 1941, the population variance of x was approximately σ2 = 5.1. Suppose a recent study of age at first marriage for a random sample of 51 women in rural Quebec gave a sample variance s2 = 2.7. Use a 5% level of significance to test the claim that the current variance is less than 5.1. Find a 90% confidence interval for the population variance.
What are the degrees of freedom?
| lower limit | |
| upper limit |
The hypotheses can be constructed as:
H0: σ2 = 5.1
H1: σ2 < 5.1
a)
The level of significance (α) = 5% that is 0.05
Sample size (n) = 51
b)
The value of the test statistic can be obtained as:
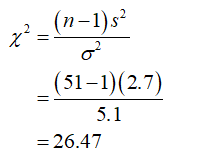
The degree of freedom = n – 1 = 51 – 1 = 50
The p value of the test statistic from the chi square table at 50 degree of freedom is 0.9975.
The p value is greater than level of significance therefore, the null hypothesis would fail to reject and it can be concluded that there is not sufficient evidence to support the claim that the current variance is less than 5.1.
Step by step
Solved in 5 steps with 3 images









