Let V₁, V₂ be vectors in R³ given by ---- V1 a) Find a vector w R³ with the following properties: • w / 0 • For any linear transformation T: R³ R³ which satisfies T(v₁) = T (V₂) we must have T(w) = 0. Enter the vector w in the form [C₁, C₂, C3]: d₁ b) Find a vector z = d₂ with the following properties: d3 Enter the vector z in the form [d₁, d₂, d3]: V2 • d₁ = 0 • For any linear transformation T: R³ R³ which satisfies T (V₁) = T(v₂) we must have T(z) = T(v₁) = T (v₂). Hint. Use part a).
Let V₁, V₂ be vectors in R³ given by ---- V1 a) Find a vector w R³ with the following properties: • w / 0 • For any linear transformation T: R³ R³ which satisfies T(v₁) = T (V₂) we must have T(w) = 0. Enter the vector w in the form [C₁, C₂, C3]: d₁ b) Find a vector z = d₂ with the following properties: d3 Enter the vector z in the form [d₁, d₂, d3]: V2 • d₁ = 0 • For any linear transformation T: R³ R³ which satisfies T (V₁) = T(v₂) we must have T(z) = T(v₁) = T (v₂). Hint. Use part a).
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![Let \(\mathbf{v_1}, \mathbf{v_2}\) be vectors in \(\mathbb{R}^3\) given by
\[
\mathbf{v_1} = \begin{bmatrix} 4 \\ 1 \\ 1 \end{bmatrix}, \quad \mathbf{v_2} = \begin{bmatrix} 3 \\ 0 \\ 3 \end{bmatrix}
\]
**a) Find a vector** \(\mathbf{w} \in \mathbb{R}^3\) **with the following properties:**
- \(\mathbf{w} \neq \mathbf{0}\)
- For any linear transformation \(T : \mathbb{R}^3 \rightarrow \mathbb{R}^3\) which satisfies \(T(\mathbf{v_1}) = T(\mathbf{v_2})\) we must have \(T(\mathbf{w}) = \mathbf{0}\).
Enter the vector \(\mathbf{w}\) in the form \([c_1, c_2, c_3]\):
\[
\begin{array}{c}
\boxed{}
\end{array}
\]
**b) Find a vector** \(\mathbf{z} = \begin{bmatrix} d_1 \\ d_2 \\ d_3 \end{bmatrix}\) **with the following properties:**
- \(d_1 = 0\)
- For any linear transformation \(T : \mathbb{R}^3 \rightarrow \mathbb{R}^3\) which satisfies \(T(\mathbf{v_1}) = T(\mathbf{v_2})\) we must have \(T(\mathbf{z}) = T(\mathbf{v_1}) = T(\mathbf{v_2})\).
*Hint. Use part a).*
Enter the vector \(\mathbf{z}\) in the form \([d_1, d_2, d_3]\):
\[
\begin{array}{c}
\boxed{}
\end{array}
\]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fb493ecdd-cbdc-400d-a05a-de2010eb2d52%2Fa3125e40-4364-4603-81c1-6ed9f23706d3%2Fz63qbed_processed.png&w=3840&q=75)
Transcribed Image Text:Let \(\mathbf{v_1}, \mathbf{v_2}\) be vectors in \(\mathbb{R}^3\) given by
\[
\mathbf{v_1} = \begin{bmatrix} 4 \\ 1 \\ 1 \end{bmatrix}, \quad \mathbf{v_2} = \begin{bmatrix} 3 \\ 0 \\ 3 \end{bmatrix}
\]
**a) Find a vector** \(\mathbf{w} \in \mathbb{R}^3\) **with the following properties:**
- \(\mathbf{w} \neq \mathbf{0}\)
- For any linear transformation \(T : \mathbb{R}^3 \rightarrow \mathbb{R}^3\) which satisfies \(T(\mathbf{v_1}) = T(\mathbf{v_2})\) we must have \(T(\mathbf{w}) = \mathbf{0}\).
Enter the vector \(\mathbf{w}\) in the form \([c_1, c_2, c_3]\):
\[
\begin{array}{c}
\boxed{}
\end{array}
\]
**b) Find a vector** \(\mathbf{z} = \begin{bmatrix} d_1 \\ d_2 \\ d_3 \end{bmatrix}\) **with the following properties:**
- \(d_1 = 0\)
- For any linear transformation \(T : \mathbb{R}^3 \rightarrow \mathbb{R}^3\) which satisfies \(T(\mathbf{v_1}) = T(\mathbf{v_2})\) we must have \(T(\mathbf{z}) = T(\mathbf{v_1}) = T(\mathbf{v_2})\).
*Hint. Use part a).*
Enter the vector \(\mathbf{z}\) in the form \([d_1, d_2, d_3]\):
\[
\begin{array}{c}
\boxed{}
\end{array}
\]
Expert Solution
Step 1
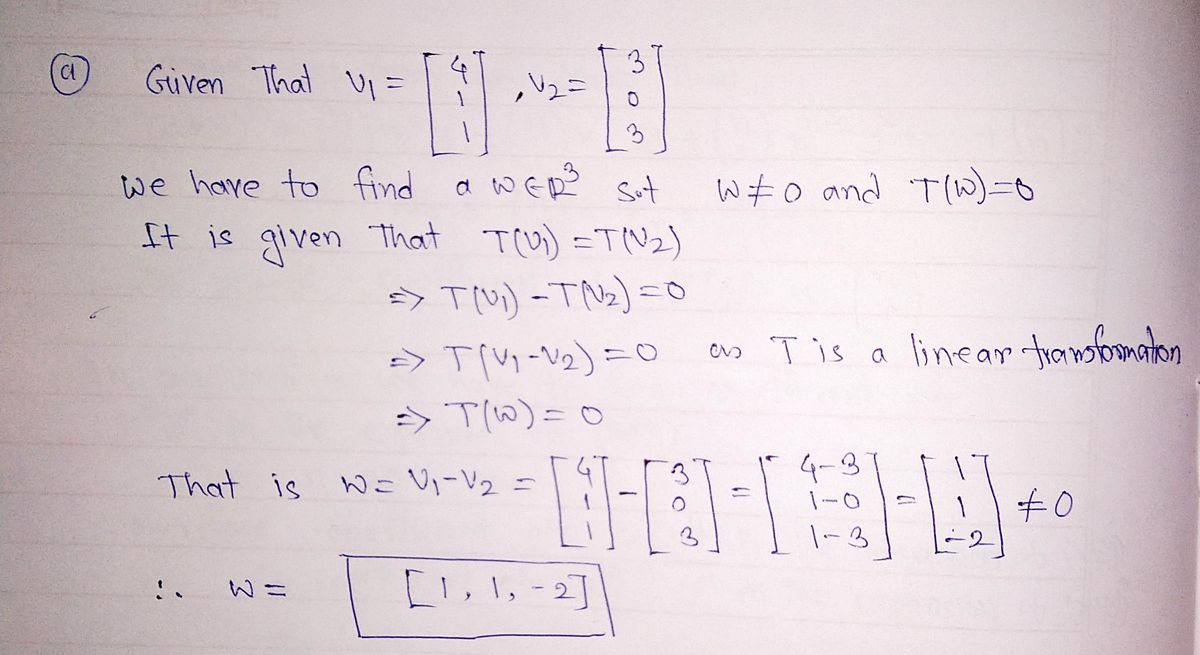
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

