Please don't format the response like this:
Now find the derivative of the given function.
h'x=dhxdx=ddxtan2x+5=sec22x+5·ddx2x+5 Apply the Chain rule=sec22x+5ddx2x+ddx5=sec22x+52·ddxx+5·ddx1=sec22x+521x1-1+50 Apply the Power law=sec22x+521+0=sec22x+52=2sec22x+5
Now find the second derivative of the given function.
h''x=d2hxdx2=ddxdhxdx=ddx2sec22x+5=2·ddxsec22x+5=2ddxsec2x+52=22sec2x+52-1·ddxsec2x+5 Apply the Chain rule=22sec2x+51sec2x+5tan2x+5·ddx2x+5 Again apply the Chain rule=22sec22x+5tan2x+5ddx2x+ddx5=22sec22x+5tan2x+52ddxx+5ddx1=22sec22x+5tan2x+521x1-1+50 Apply the Power law=22sec22x+5tan2x+52=8sec22x+5tan2x+5
Therefore,
h'x=2sec2(2x+5)h''x=8sec2(2x+5)tan(2x+5)
It is difficult to read when I don't understand the problem and want to learn

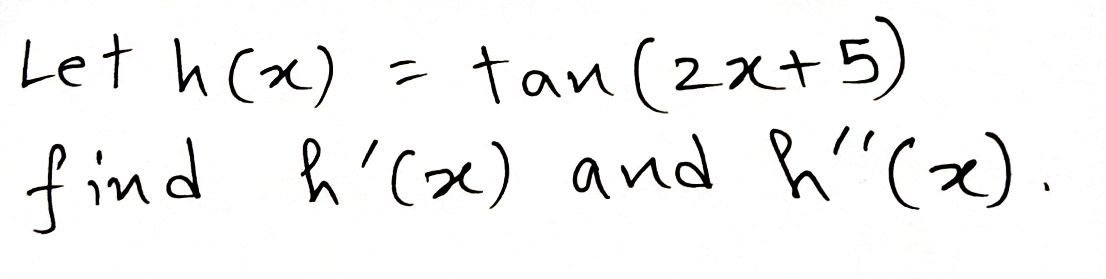
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images









