Let $X$ be a set and assume that p E X. Let Tp be the collection 0, X, and all subsets of X that exclude n
Let $X$ be a set and assume that p E X. Let Tp be the collection 0, X, and all subsets of X that exclude n
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:**Statement:**
Show that \( \mathcal{T}_p \) is a topology on \( X \).
---
**Explanation:**
To establish that \( \mathcal{T}_p \) is a topology on the set \( X \), you must verify the following three conditions:
1. **The Empty Set and \( X \):** Both the empty set \( \emptyset \) and the set \( X \) must be in \( \mathcal{T}_p \).
2. **Closed Under Arbitrary Unions:** The collection \( \mathcal{T}_p \) must be closed under arbitrary unions. This means that for any collection of sets \(\{U_i\}\) where each \(U_i\) is in \( \mathcal{T}_p \), the union \(\bigcup U_i\) must also be in \( \mathcal{T}_p \).
3. **Closed Under Finite Intersections:** The collection \( \mathcal{T}_p \) must be closed under finite intersections. This implies that for any finite collection of sets \(\{U_1, U_2, \ldots, U_n\}\) where each \(U_i\) is in \( \mathcal{T}_p \), the intersection \(\bigcap_{i=1}^n U_i\) must also be in \( \mathcal{T}_p \).
These conditions ensure that \( \mathcal{T}_p \) is indeed a topology on \( X \).

Transcribed Image Text:Let \( X \) be a set and assume that \( p \in X \). Let \( \mathcal{T}_p \) be the collection \(\emptyset, X\), and all subsets of \( X \) that exclude \( p \).
Expert Solution
Step 1
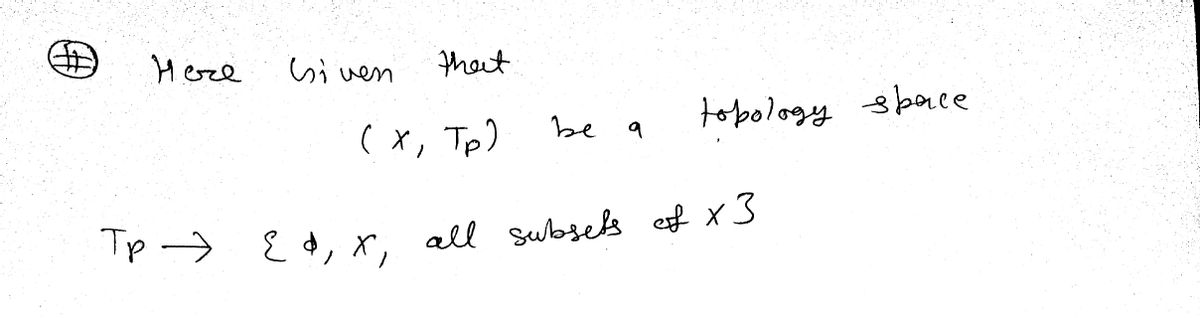
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

