Let a body of mass m = 1 kg be dropped from a height by an inclined plane that forms an angle a = 15 ° with the horizontal, which has a length OA = 2 m and a coefficient of friction 4 = 0.15. Then it continues along a horizontal plane also of length d = 2 m and with friction coefficient pz = 0.1. At the end of this plane it collides with a pendulum of mass M = 2 kg and length L = 2 m. As a result of the collision the body of mass "m" stops and the pendulum starts moving. It is required: a) Body speed "m" when reaching the end of the inclined plane. b) Body speed "m" when reaching the end of the horizontal plane. c) Speed of the pendulum of mass "M" just after the collision.
Let a body of mass m = 1 kg be dropped from a height by an inclined plane that forms an angle a = 15 ° with the horizontal, which has a length OA = 2 m and a coefficient of friction 4 = 0.15. Then it continues along a horizontal plane also of length d = 2 m and with friction coefficient pz = 0.1. At the end of this plane it collides with a pendulum of mass M = 2 kg and length L = 2 m. As a result of the collision the body of mass "m" stops and the pendulum starts moving. It is required: a) Body speed "m" when reaching the end of the inclined plane. b) Body speed "m" when reaching the end of the horizontal plane. c) Speed of the pendulum of mass "M" just after the collision. d) Is the elastic shock? e) Maximum height "h" reached by the pendulum and the value of angle 0 formed by the pendulum cable with the vertical at that point. (See figure) Note Define precisely all the physical quantities used. In mathematical developments clearly justify the steps.% 3D m-1 kg d = 2 m L = 2 m0 A = 15 ° M = 2kg AB d = 2 m

Consider the motion from top of the incline to the bottom of the incline
From Work-energy theorem.
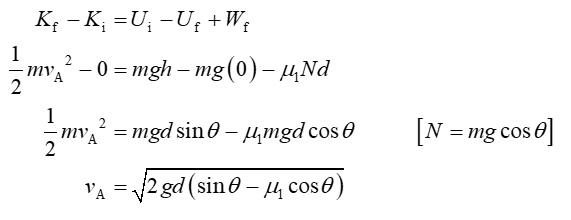
Substitution
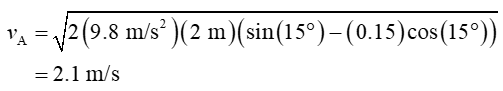
(b) Consider the motion from point A to B.
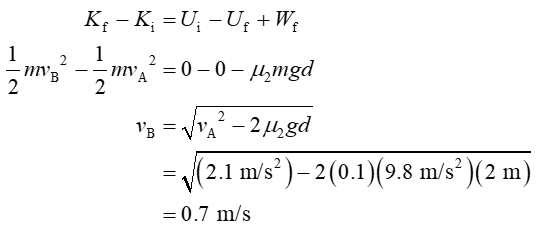
Step by step
Solved in 6 steps with 5 images
