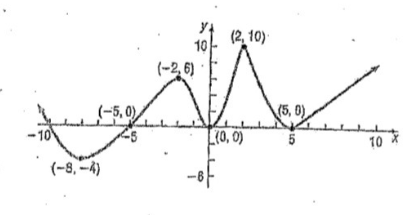
Isf increasing on the interval (-8,-2) ? Is f increasing on the interval (2, 10) ? List the interval(s) on which f is increasing. Is there a local maximum at 2? If yes, what is it? List the numbers at which f has a local maximum. What are the local maxium? (-5,0), (-8,-4) (-2,6) Chuchl (2, 10). (0, 0) (5,0) 5 10 X
Isf increasing on the interval (-8,-2) ? Is f increasing on the interval (2, 10) ? List the interval(s) on which f is increasing. Is there a local maximum at 2? If yes, what is it? List the numbers at which f has a local maximum. What are the local maxium? (-5,0), (-8,-4) (-2,6) Chuchl (2, 10). (0, 0) (5,0) 5 10 X
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:**Educational Text Transcription**
### Questions:
1. Is \( f \) increasing on the interval \( (-8, -2) \)?
2. Is \( f \) increasing on the interval \( (2, 10) \)?
3. List the interval(s) on which \( f \) is increasing.
4. Is there a local maximum at 2? If yes, what is it?
5. List the numbers at which \( f \) has a local maximum.
6. What are the local maximum?
### Graph Explanation:
The graph provided is a plot of a function \( f(x) \) on a Cartesian plane with labeled points and intervals. The x-axis ranges from -10 to 10 and the y-axis from -6 to 10.
- The function starts at point \((-8, -4)\) and rises to point \((-5, 0)\), indicating an increase.
- From \((-5, 0)\) to \((-2, 6)\), the function continues to increase, reaching a peak at \((-2, 6)\), which is a local maximum.
- It then decreases to the origin \((0, 0)\).
- The function again increases from the origin to the point \((2, 10)\), which is another local maximum.
- After peaking at \((2, 10)\), the function decreases to \((5, 0)\).
- Finally, the function increases from \((5, 0)\) onward.
**Key Observations:**
- **Intervals where \( f \) is increasing:** \((-8, -2)\), \((0, 2)\), and \((5, 10)\).
- **Local Maximum Points:** \((-2, 6)\) and \((2, 10)\).
- The function does not have a local maximum at \( x = 2 \) based on the given graph, as it is a local maximum at \( x = 2 \).
This graph and the questions are designed to test understanding of function behavior, especially the concept of increasing intervals and local maxima in calculus.
Expert Solution
Step 1: Description of given data
We have given:
Given graph is said to be increasing or decreasing on the given interval in which or
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 21 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

