Is the following total differential exact? df(g,h) = 7g(g^3+ h^2)jdg + 2h^4(3g^2 + 7h^2)jdh. Could this total differential describe a state function?
Q: Consider a quantum system in the initial state ly (0) = |x,) at r = 0, and the Hamiltonian H = (252…
A: Given:Initial state; ∣ψ(0)⟩=∣x+⟩Hamiltonian; H=(2ℏΩ00ℏΩ)Constant frequency; Ω We can express the…
Q: Consider a three-dimensional infinite well modeled as a cube of side L. The width L of the cube is…
A: Given: The width of the cube is L The ground state energy of the electron is E0
Q: A particle of mass m is bound in a one-dimensional well with one impenetrable wall. The potential…
A:
Q: (20.7) The energy E of a system of three independent harmonic oscillators is given by 1 E = (Nx + ½…
A:
Q: Consider the elements Zinc (Zn) and Gallium (Ga). Their atomic mass, density and electronic shell…
A: Given: We have to find fermi energy of zinc and gallium.
Q: A particle of mass m, which moves freely inside an infinite potential well of length a, is initially…
A: Given: ψ(x,0)=35asin3πxa+15a sin5πxa For the wavefunction at a later time t we have;…
Q: Four particles A, B, C and D are distributed in four energy levels E, =0 , E, =ɛ Ez =28 E3 =38 It is…
A:
Q: 1. Consider a system of N localized non-interacting 1 – d quantum harmonic oscillators with…
A: We have to write the partition function is simple harmonic oscillator and also find its specific…
Q: A spin 1/2 system is known to be in an eigenstate of Sn (Sa+S₂)/√2 with eigenvalue +ħ/2. Find the…
A:
Q: A measurement of the magnitude of Sx for the spin 1/2 system produces an eigenvalue
A: There are scalar values called Eigenvalues associated with linear equations in the matrix equations,…
Q: 1. Returning to our old favorite, an infinite square potential is defined by I L: U (x) = ∞ As we've…
A: Given wave function in region Else it is zero.
Q: The coupling efficiency will also depend on whether the Numerical Apertures of the focussed laser…
A: GivenThe coupling efficiency will also depend on whether the Numerical Apertures of the focussed…
Q: A quantum mechanical particle is confined to a one-dimensional infinite potential well described by…
A: Step 1: Given: Particle in a 1-D infinite potential well described by the potential:V(x) =0,…
Q: An atom has energy levels 0, E, 2E, Calculate the canonical partition function of a system composed…
A: The canonical partition function for an atom is given by, Where, gi be defined as the degeneracy of…
Q: structure
A:
Q: By determining the temperature at which the magnetic moment vanishes for a two- dimensional Ising…
A: Based on the information provided in the image and the knowledge of projectile motion, here's how to…
Q: explain the Fermi Dirac distribution
A: Explain the Fermi Dirac distribution
Q: Evaluate the transmission coefficient for a rectangular barrier with a potential given by Vo, (-a <x…
A:
Is the following total differential exact? df(g,h) = 7g(g^3+ h^2)jdg + 2h^4(3g^2 + 7h^2)jdh. Could this total differential describe a state function?
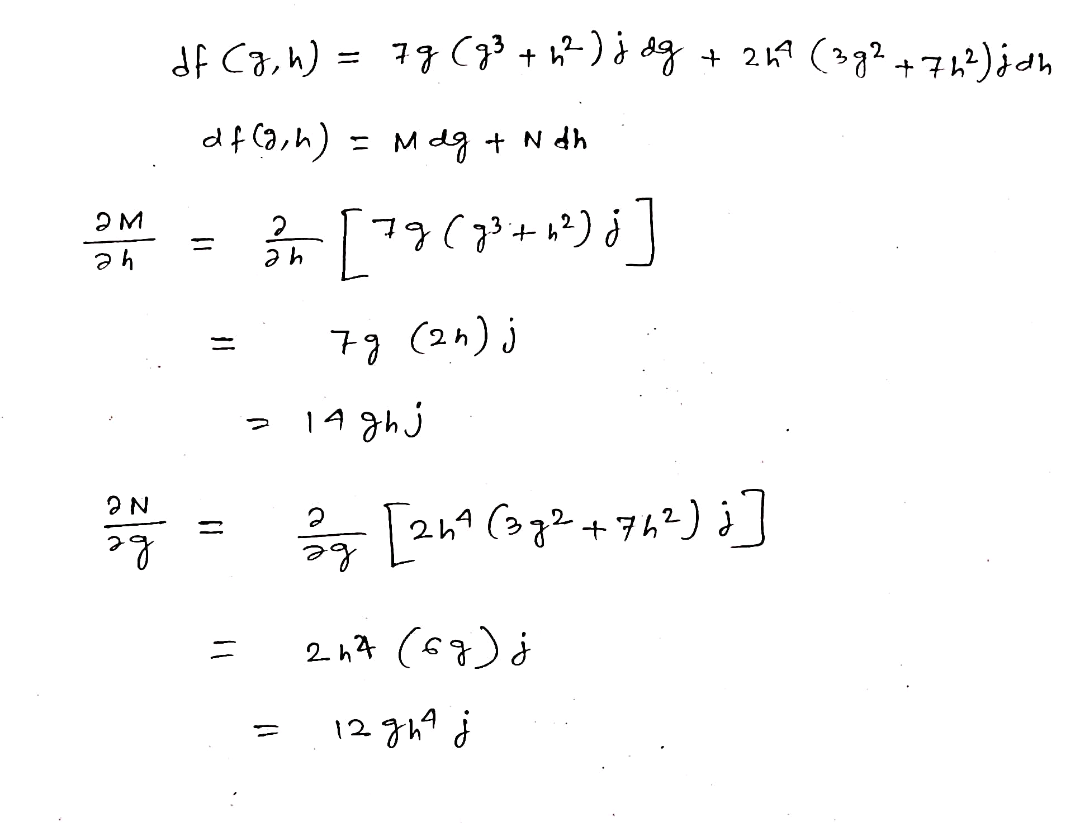
Step by step
Solved in 2 steps with 2 images

- The value of a partition function roughly represents the maximum energy of the states at a given temperature. O True FalseA conduction electron is confined to a metal wire of length (1.46x10^1) cm. By treating the conduction electron as a particle confined to a one-dimensional box of the same length, find the energy spacing between the ground state and the first excited state. Give your answer in eV. Note: Your answer is assumed to be reduced to the highest power possible. Your Answer: x10 AnswerI need solution question 7
- The Morse oscillator modeling a different diatomic molecule has D = 384 kJ/mole and hw = 1240 cm-¹. (Again, 11.9627 J/mole = 1 cm ¹.) ✓ нал (a) What is the energy of the pictured eigenfunction? Report the energy in cm¹ above the minimum in the potential well. (b) How close to the dissociation limit is this state in kJ/mole, that is, what is the energy difference between this state and molecular dissociation?4. a) Consider a square potential well which has an infinite barrier at x = 0 and a barrier of height U at x = L, as shown in the figure. For the case E L) that satisfy the appropriate boundary conditions at x = 0 and x = o. Put the appropriate conditions on x = L to find the allowed energies of the system. Are there conditions for which the solution is not possible? explain. U E L.Consider the sheet formed by the intersection of the curves: x = 0, x = 4, y = 0, y = 3 [=] cm, with a variable density of mass per unit area ρ(x,y) = xy [=] g/cm2 . Write and evaluate multiple integrals to calculate the following: a. The area of the sheet [=] cm2 . b. The mass of the sheet [=] g. c. The shell moments about the x & y axes (Mx & My) [=] g∙cm. d. The position of the center of mass of the sheet ( , ) [=] cm.