is "3!", the existential quantifier foll DEFINITION: For an open sentence p(x) and a set S, "(! x S) (p(x))" (read "there is a nique x in S such that p(x)") means: (3x ES) (p(x)) and (Vu, vES) ([p(u) and p(v)] ⇒ u = v). a) Explain, in intuitive terms, how "(3! x S) (p(x))" says that there is exactly one ele- ment from S in the truth set of p(x).
is "3!", the existential quantifier foll DEFINITION: For an open sentence p(x) and a set S, "(! x S) (p(x))" (read "there is a nique x in S such that p(x)") means: (3x ES) (p(x)) and (Vu, vES) ([p(u) and p(v)] ⇒ u = v). a) Explain, in intuitive terms, how "(3! x S) (p(x))" says that there is exactly one ele- ment from S in the truth set of p(x).
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Question a
![Certainly! Here is the transcription and explanation suitable for an educational website:
---
**Unique Existence Quantifier**
There is a third quantifier, called the "unique existence" quantifier, which is used to abbreviate statements like the definition of "function" (Definition 3.14). The symbol for this quantifier is "∃!", the existential quantifier followed by an exclamation point. It is defined as follows.
**Definition:** For an open sentence \( p(x) \) and a set \( S \), "\( (\exists! x \in S) (p(x)) \)" (read "there is a unique \( x \) in \( S \) such that \( p(x) \)") means:
\[
(\exists x \in S) (p(x)) \quad \text{and} \quad (\forall u, v \in S) ([p(u) \quad \text{and} \quad p(v)] \Rightarrow u = v)
\]
a) Explain, in intuitive terms, how "\( (\exists! x \in S) (p(x)) \)" says that there is exactly one element from \( S \) in the truth set of \( p(x) \).
---](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fc06c0cac-2e9c-4d45-9a45-e5decd8c209b%2F3fd5b1de-bcd2-456d-9b7f-c10b7366846f%2Fyxl46sr_processed.jpeg&w=3840&q=75)
Transcribed Image Text:Certainly! Here is the transcription and explanation suitable for an educational website:
---
**Unique Existence Quantifier**
There is a third quantifier, called the "unique existence" quantifier, which is used to abbreviate statements like the definition of "function" (Definition 3.14). The symbol for this quantifier is "∃!", the existential quantifier followed by an exclamation point. It is defined as follows.
**Definition:** For an open sentence \( p(x) \) and a set \( S \), "\( (\exists! x \in S) (p(x)) \)" (read "there is a unique \( x \) in \( S \) such that \( p(x) \)") means:
\[
(\exists x \in S) (p(x)) \quad \text{and} \quad (\forall u, v \in S) ([p(u) \quad \text{and} \quad p(v)] \Rightarrow u = v)
\]
a) Explain, in intuitive terms, how "\( (\exists! x \in S) (p(x)) \)" says that there is exactly one element from \( S \) in the truth set of \( p(x) \).
---
Expert Solution
Step 1
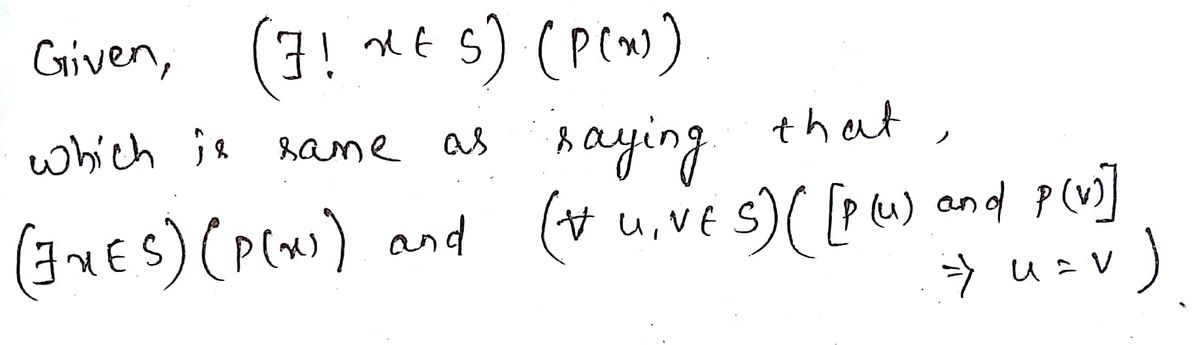
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

