Investigate the dependence of pV on V for real gases.
In case of ideal gas product of pressure and volume in isothermal process remains constant as:
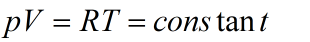
for 1 mole of gas. For real gas the case is different.
To Investigate the dependence of pV on V for real gases, write the Vander waal equation as:
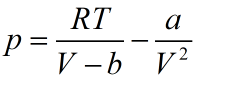
Also written as:
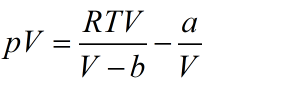
Figure out the product of pV for relative extrema. So, derivative of pV with respect to V is,
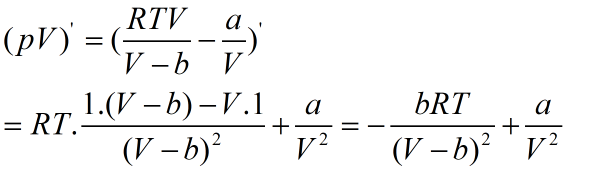
Equating derivative to zero, gives the critical points as:
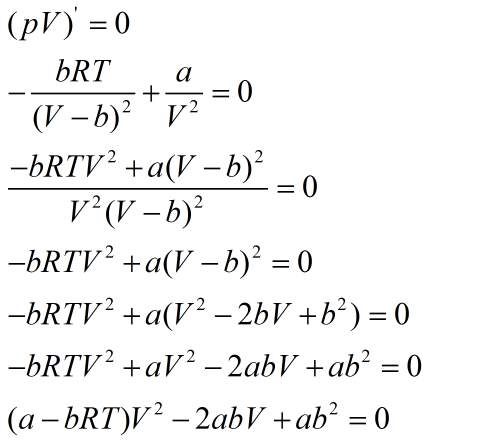
Quadratic equation is obtained whose discriminant is equal to zero.

As discriminant is always positive, a quadratic equation has two roots as given:
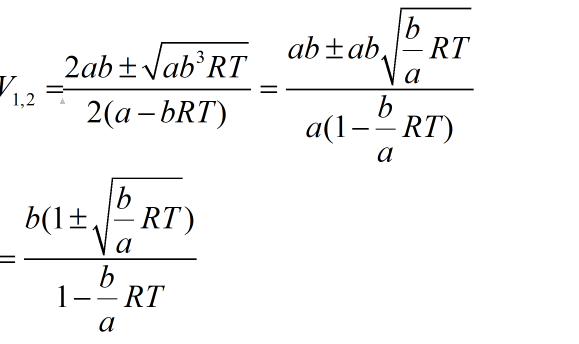
Root 1 with negative sign in numerator has no meaning as V1<b
So pV has extremum at:

Provided as 1-b/a RT >0, the branches of parabola represents the numerator of derivative which will be directed upwards. So sign of derivative changes from minus to plus when going through root V2. This tells that V2 is minima point of function pV: V2= Vmin.
So when vander waal gas is compressed at constant temperature product pV initially decreases the attain a minimum value of pV min then again rise. First step can be explained by dominating attractive forces between molecules and second with increased contribution of repulsive forces.
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 11 images









