induction question7
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
induction question7
![1. Prove by contradiction that 6n + 5 is odd for all integers n.
2. Prove that for all integers n, if 3n + 5 is even then n is odd. (Hint: prove the contra-
positive)
3. Prove that
|x + y| < ]x| + \y]
for all real numbers x and
Y.
4. Prove that there does not exist a smallest positive real number. (In other words, prove
that there does not exist a positive real number x such that x < y for all positive real
numbers y).
5. Recall that an irrational number is a real number which is not rational. Prove that
if x is rational and y is irrational, then x+y is irrational. You may use the fact that
the rational numbers are closed under addition - if a and b are rational numbers, then
a + b is rational as well.
6. Prove that if a, b, and c are positive real numbers with ab = c, then a <Vc or b < Vc.
7. Prove that
1
i=1
for all positive integers n.
8. Prove that
i · i! = (n+ 1)! – 1
i=1
for all positive integers n.
9. Prove that
2" < n!
for all positive integers n such that n > 4.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F67a79aa2-f715-406c-8bee-8178252bb86d%2F38392018-2901-4e3d-a1c6-11c542999eed%2Fz2m4wvg_processed.jpeg&w=3840&q=75)
Transcribed Image Text:1. Prove by contradiction that 6n + 5 is odd for all integers n.
2. Prove that for all integers n, if 3n + 5 is even then n is odd. (Hint: prove the contra-
positive)
3. Prove that
|x + y| < ]x| + \y]
for all real numbers x and
Y.
4. Prove that there does not exist a smallest positive real number. (In other words, prove
that there does not exist a positive real number x such that x < y for all positive real
numbers y).
5. Recall that an irrational number is a real number which is not rational. Prove that
if x is rational and y is irrational, then x+y is irrational. You may use the fact that
the rational numbers are closed under addition - if a and b are rational numbers, then
a + b is rational as well.
6. Prove that if a, b, and c are positive real numbers with ab = c, then a <Vc or b < Vc.
7. Prove that
1
i=1
for all positive integers n.
8. Prove that
i · i! = (n+ 1)! – 1
i=1
for all positive integers n.
9. Prove that
2" < n!
for all positive integers n such that n > 4.
Expert Solution
Step 1
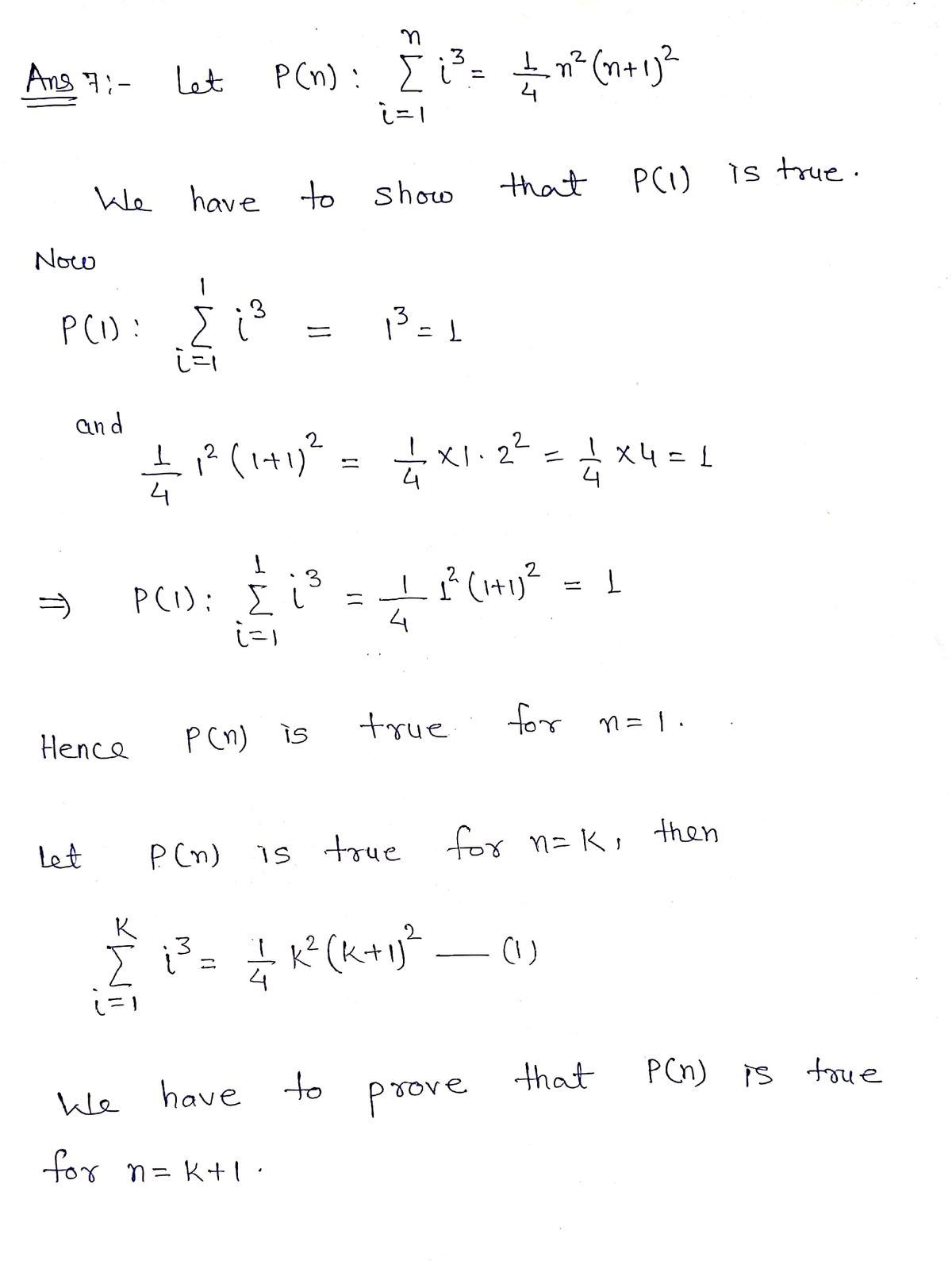
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

