How could you solve this? Independent random samples of professional football and basketball players gave the following information. Assume that the weight distributions are mound-shaped and symmetric.Weights (in Ib) of pro football players: x1; n1 = 21248 261 255 251 244 276 240 265 257 252 282256 250 264 270 275 245 275 253 265 271Weights (in Ib) of pro basketball players: x2; n2 = 19205 200 220 210 192 215 223 216 228 207225 208 195 191 207 196 181 193 201(a) Use a calculator with mean and standard deviation keys to calculate x1, S1, X2, and s3. (Round your answers to one decimal place.)X1 =S1 =X2 =S2 =(b) Let 41 be the population mean for x1 and let u2 be the population mean for x2. Find a 99% confidence interval for u1 - H2: (Round your answers to one decimal place.)lower limitupper limit

Name: How could you solve this? Independent random samples of professional f
Uploaded: 2024-03-20T07:06:27.000Z
Channel: Bartleby
Description: How could you solve this? Independent random samples of professional football and basketball players gave the following information. Assume that the weight distributions are mound-shaped and symmetric.Weights (in Ib) of pro football players: x1; n1 =

Answered: Independent random samples of…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Concept explainers

Topic Video

Question

How could you solve this?

Independent random samples of professional football and basketball players gave the following information. Assume that the weight distributions are mound-shaped and symmetric.
Weights (in Ib) of pro football players: x1; n1 = 21
248 261 255 251 244 276 240 265 257 252 282
256 250 264 270 275 245 275 253 265 271
Weights (in Ib) of pro basketball players: x2; n2 = 19
205 200 220 210 192 215 223 216 228 207
225 208 195 191 207 196 181 193 201
(a) Use a calculator with mean and standard deviation keys to calculate x1, S1, X2, and s3. (Round your answers to one decimal place.)
X1 =
S1 =
X2 =
S2 =
(b) Let 41 be the population mean for x1 and let u2 be the population mean for x2. Find a 99% confidence interval for u1 - H2: (Round your answers to one decimal place.)
lower limit
upper limit

Expert Solution

Step 1

(a)

Mean and standard deviation for $x_{1}$ :

Use Ti 83 calculator to find the mean and standard deviation as follows:

Select STAT > Edit > Enter the values of as L1.
Click $2^{n d}$ button; STAT; take the arrow to the MATH menu, and then ‘3’ numbered key.
Click $2^{n d}$ button; then ‘1’ numbered key to get L1, and close the ‘)’ bracket.
Click Enter.
Click $2^{n d}$ button; STAT; take the arrow to the MATH menu, and then ‘7’ numbered key.
Click $2^{n d}$ button; then ‘1’ numbered key to get L1, and close the ‘)’ bracket.
Click Enter.

Output using Ti 83 calculator is given below:

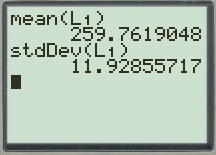
From the Ti 83 calculator output, the mean value is 259.8, and standard deviation value is 11.9.

Thus, ${\bar{x}}_{1} = 259.8, s_{1} = 11.9$ .

Mean and standard deviation for $x_{2}$ :

Use Ti 83 calculator to find the mean and standard deviation as follows:

Select STAT > Edit > Enter the values of as L2.
Click $2^{n d}$ button; STAT; take the arrow to the MATH menu, and then ‘3’ numbered key.
Click $2^{n d}$ button; then ‘2’ numbered key to get L2, and close the ‘)’ bracket.
Click Enter.
Click $2^{n d}$ button; STAT; take the arrow to the MATH menu, and then ‘7’ numbered key.
Click $2^{n d}$ button; then ‘2’ numbered key to get L2, and close the ‘)’ bracket.
Click Enter.

Output using Ti 83 calculator is given below:

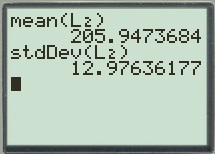
From the Ti 83 calculator output, the mean value is 205.9, and standard deviation value is 13.0.

Thus, ${\bar{x}}_{2} = 205.9, s_{2} = 13.0$ .

Trending now

This is a popular solution!

Step by step

Solved in 2 steps with 2 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Data Collection, Sampling Methods, and Bias$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Similar questions