Is the set S linearly independent? b. Is v = (1, -2, 1) in the span of S? If not, show why not. If so, give the coefficients c1, c2, c3 needed to show v can be written as a linear combination of the
Consider the set, S = {(5, 0, 2), (10, 0, 7), (0, 3, 0)}
Answer the following questions. Your work must clearly show the justification of your conclusion. There are various methods that this can be done (some can be combined to answer more than one question). Be sure to cite any theorems or definitions. Give your conclusion in a complete sentence. Be sure your answer connects all the dots to lead to that conclusion.
For this question, you may use technology to fill in the gaps for any computations (i.e. for finding a determinant or putting a matrix in reduced row echelon form); you must state what technology you used and for what purpose. Be sure you show the statements that are bridged by your technology -- such as the original matrix and then the RRE form.
a. Is the set S linearly independent?
b. Is v = (1, -2, 1) in the span of S? If not, show why not. If so, give the coefficients c1, c2, c3 needed to show v can be written as a linear combination of the
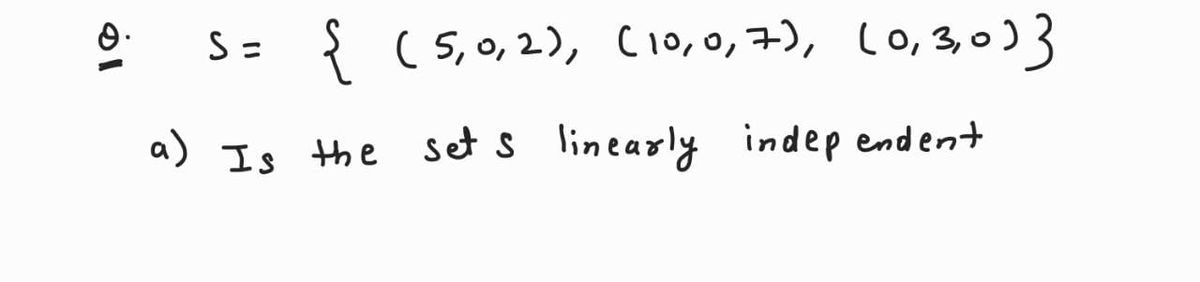
Step by step
Solved in 2 steps with 2 images

In part a I dont know what rank A is? can you elabrolate?








