In his writings, Alexander Hamilton used the word 'upon' an average of 3.24 times per thousand words. Let X = the number of times 'upon' is used in a randomly selected 1000 words of Alexander HamiltonOs writings. X may be modeled as a Poisson random variable with parameter A = 3.24. Let Y equal the number of times 'upon' is used in a randomly selected 3000 words of Alexander HamiltonOs writings. a. For our model, what is expected value of X? b. What is the probability that X = 3? c. What is the probability that X < 6?
Contingency Table
A contingency table can be defined as the visual representation of the relationship between two or more categorical variables that can be evaluated and registered. It is a categorical version of the scatterplot, which is used to investigate the linear relationship between two variables. A contingency table is indeed a type of frequency distribution table that displays two variables at the same time.
Binomial Distribution
Binomial is an algebraic expression of the sum or the difference of two terms. Before knowing about binomial distribution, we must know about the binomial theorem.

Note- As per our policy we can answer only the first 3 sub-parts of a question. If you want solutions for other parts also, then you have to make a separate request.
Given information-
We have given the problem of Poisson distribution.
Mean, λ = 3.24
X = Poisson random variable
PMF of this distribution is-
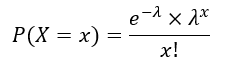
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 3 images




