In class we did a problem where we saw that Planck’s law, which is given by I(λ, T) = 2πhc2 λ5(e hc/λkbT − 1) , at high wavelengths reduces to the classical prediction I(λ, T) = 2πckBT λ4 . We did this by using the MacLaurin series for an exponential. 1 + x + x 2 2! + x 3 3! + x 4 4! + ... When we did this problem in class, we reasoned that,when the wavelength (λ) is large, the term hc/λkbT is small enough that any term (hc/λkbT) 2 or (hc/λkbT) 3 or any higher power is neglible. That’s how we showed that, in the limit of large λ, Planck’s law reduces to the classical prediction. Now assume that we want to make a slightly better approximation. We still assume that λ is large and therefore (hc/λkbT) 3 and (hc/λkbT) 4 and all higher powers are negligible, but now we want to work at the level of precision where (hc/λkbT) 2 is not negligible. What does Planck’s law reduce to in this case?
: In class we did a problem where we saw that Planck’s law, which is given by
I(λ, T) = 2πhc2
λ5(e
hc/λkbT − 1)
,
at high wavelengths reduces to the classical prediction
I(λ, T) = 2πckBT
λ4
.
We did this by using the MacLaurin series for an exponential.
1 + x +
x
2
2! +
x
3
3! +
x
4
4! + ...
When we did this problem in class, we reasoned that,when the wavelength (λ) is large, the term hc/λkbT
is small enough that any term (hc/λkbT)
2 or (hc/λkbT)
3 or any higher power is neglible. That’s how we
showed that, in the limit of large λ, Planck’s law reduces to the classical prediction. Now assume that we
want to make a slightly better approximation. We still assume that λ is large and therefore (hc/λkbT)
3 and
(hc/λkbT)
4 and all higher powers are negligible, but now we want to work at the level of precision where
(hc/λkbT)
2
is not negligible. What does Planck’s law reduce to in this case?
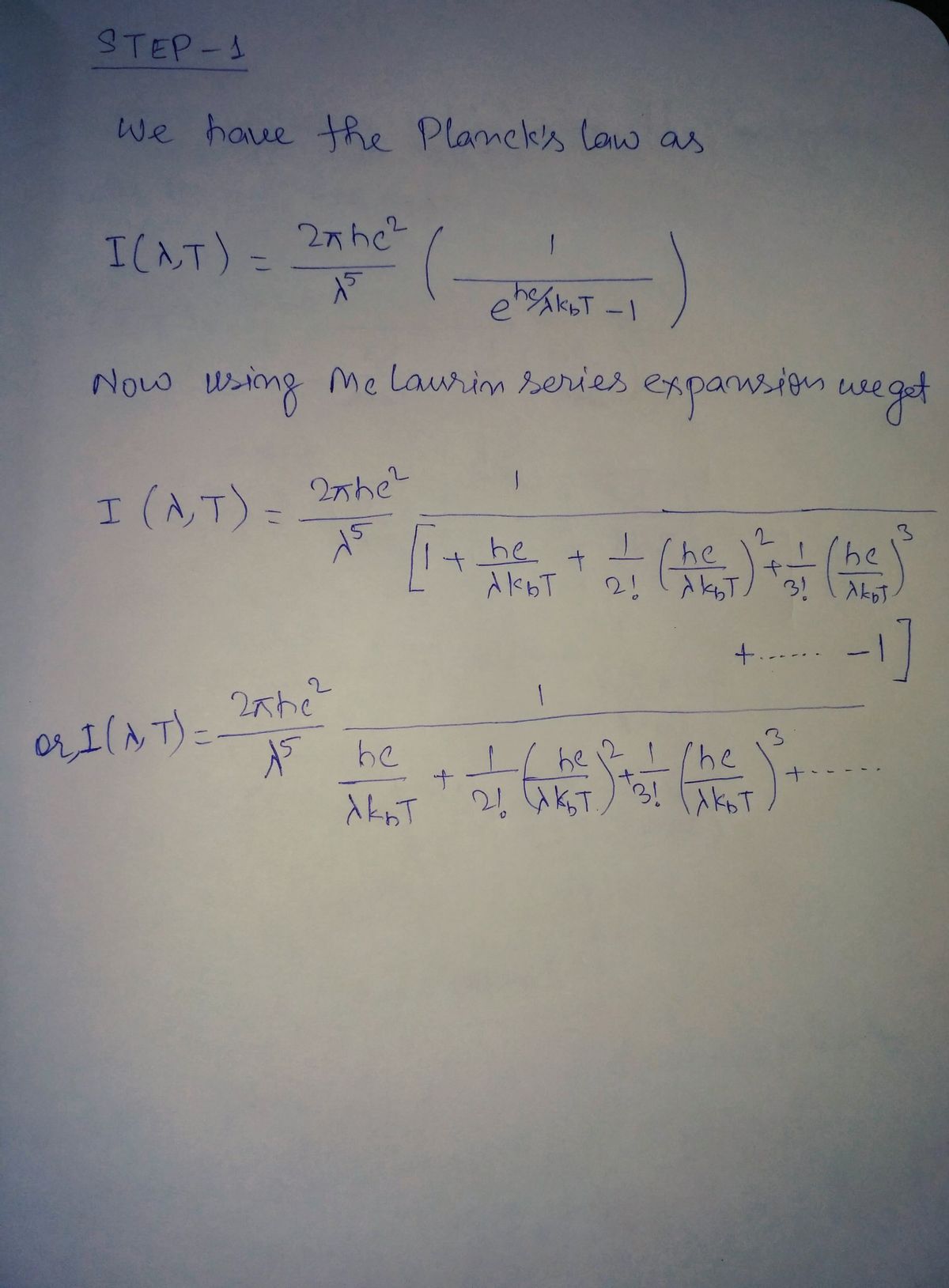
Step by step
Solved in 2 steps with 2 images
