If string 4 is improperly tuned, so that it plays 5.2 Hz too low, what is the actual wave speed in the string? Do you need to increase or decrease the speed to get the note in tune? By how much must v change?
If string 4 is improperly tuned, so that it plays 5.2 Hz too low, what is the actual wave speed in the string? Do you need to increase or decrease the speed to get the note in tune? By how much must v change?
Related questions
Question
please answer question #3
answer to first chart is in second image

Transcribed Image Text:For string 1
f=82.4 Hz , L=0.65 mf=v2Lv=2fLv=2×82.4×0.65v=107.12 m/s
For string 2
v=2x110x0.65v=143 m/s
For string 3
v=2×146.8×0.65v=190.84 m/s
For string 4
v=2x196x0.65v=254.8 m/s
For string 5
v=246.9×2x0.65v=320.97 m/s
For string 6
v=2×329.6×0.65v=428.48 m/s

Transcribed Image Text:Wave speed
(m/s)
String
Note
Frequency
(Hz)
1
82.4
E2
A2
D3
G3
110.0
3
146.8
4
196.0
B3
246.9
6.
E4
329.6
Use the frequency equation to calculate the wave speed v in each string.
2. Say that string 2 is improperly tuned, so that its wave speed is 11 m/s faster than the ideal
speed you calculated in Question 1. What frequency would it produce? Is that
frequency too high (“sharp") or too low ("flat")? By how many Hz is the note out of
tune?
3. If string 4 is improperly tuned, so that it plays 5.2 Hz too low, what is the actual wave
speed in the string? Do you need to increase or decrease the speed to get the note in
tune? By how much must v change?
Now let's consider the placement of the frets. We will use String 3, though the same
pattern works for all strings.
At its full length of L = 0.650 m, String 3 produces a frequency of 146.8 Hz (a D). To
play other notes, we need to put frets at the right positions to produces notes in half-step
increments (D#, E, F, etc.). There are the first few higher frequencies we want String 3 to
produce.
Note
Frequency (Hz)
Length (m)
1
D
146.8
0.650
Оpen
D#
155.6
Fret 1
3
E
164.8
Fret 2
4
F
174.6
Fret 3
5
F#
185.0
Fret 4
6.
G
196.0
Fret 5
Expert Solution
Step 1
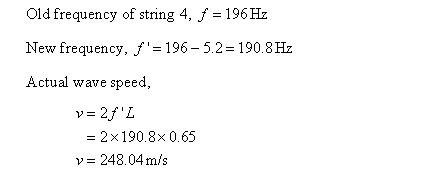
Step by step
Solved in 2 steps with 2 images
