8. Answer the following questions about the functions whose derivatives are given below. What are the critical points of f? On what open intervals is f increasing or decreasing? At what points, if any, does f assume local maximum and minimum values? a. f'(x) = x(x - 1) i. ii. 111.
8. Answer the following questions about the functions whose derivatives are given below. What are the critical points of f? On what open intervals is f increasing or decreasing? At what points, if any, does f assume local maximum and minimum values? a. f'(x) = x(x - 1) i. ii. 111.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
can you explain how i would find the following 3 points about the function and alos give me the answer. most importantly i need explanation to answer for step I, II , III the function .thanks

Transcribed Image Text:8. Answer the following questions about the functions whose derivatives are given
below.
What are the critical points of f?
On what open intervals is f increasing or decreasing?
At what points, if any, does f assume local maximum and minimum values?
a. f'(x) = x(x - 1)
i.
ii.
111.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 4 steps with 2 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
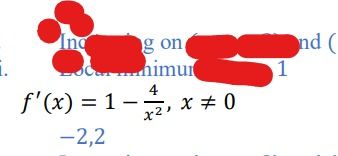
Transcribed Image Text:Ing
g on
...himur
4
f'(x) = 1 -2, x ±0
-2,2
1
nd (
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

