I Find sin 0. B 1 (-7,-8) ?]√[
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
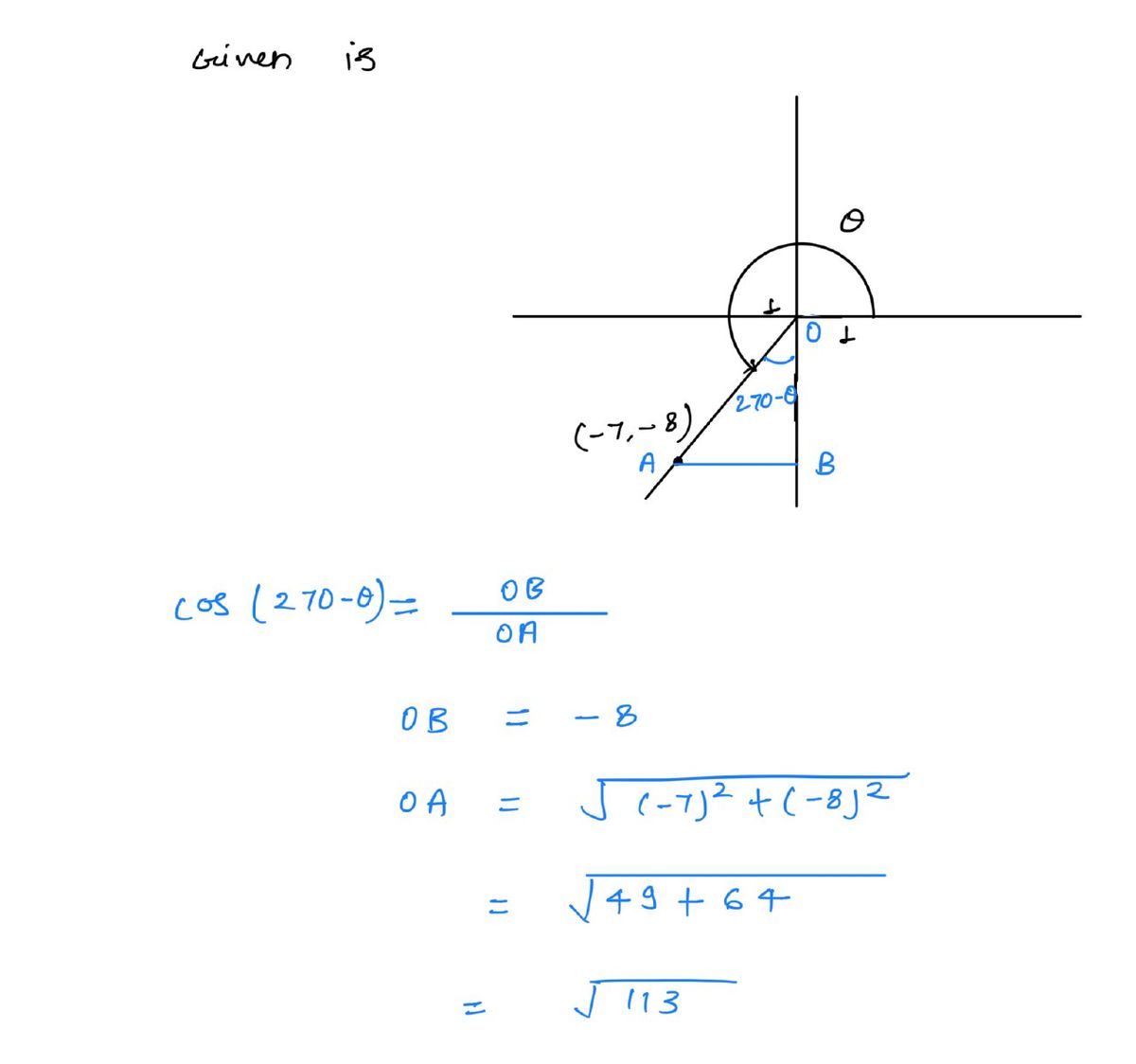
![**Title: Find \( \sin \theta \).**
**Description:**
The image shows a coordinate grid with a point located at (-7, -8) and an angle \( \theta \) measured from the positive x-axis. The radius of the circle is 1, forming a right triangle with the hypotenuse extending to the point (-7, -8).
The task is to find the sine of the angle \( \theta \), denoted as \( \sin \theta \).
**Diagram Explanation:**
1. **Coordinate System and Triangle:**
- The graph displays a quadrant of the Cartesian coordinate plane.
- A right triangle is formed with the origin (0, 0), the point (-7, -8), and the projection of this point onto the x-axis, which is (-7, 0).
2. **Points:**
- **Origin (0, 0):** Where the x and y axes intersect.
- **Point (-7, -8):** The terminal side of the angle passes through this point.
3. **Side Lengths of the Triangle:**
- Horizontal leg (adjacent to \( \theta \)): 7 units (from the x-projection to the point).
- Vertical leg (opposite to \( \theta \)): 8 units (from the y-projection).
4. **Hypotenuse:**
- Computed using the Pythagorean theorem:
\[
\text{hypotenuse} = \sqrt{(-7)^2 + (-8)^2} = \sqrt{49 + 64} = \sqrt{113}
\]
5. **Finding \( \sin \theta \):**
- The sine of the angle \( \theta \) is equal to the ratio of the length of the opposite side to the hypotenuse:
\[
\sin \theta = \frac{-8}{\sqrt{113}}
\]
**Note:**
- The negative sign in the sine function indicates the angle is below the x-axis, given its position in this quadrant of the circle.
**Interactive Portion:**
- A user input box for submitting the calculated value of \( \sin \theta \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F12b7d8e5-e1f4-4366-964c-d88f3b8c0c01%2F1477b438-75bc-46cb-b83b-93f67c0f6d91%2F5h99639_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Title: Find \( \sin \theta \).**
**Description:**
The image shows a coordinate grid with a point located at (-7, -8) and an angle \( \theta \) measured from the positive x-axis. The radius of the circle is 1, forming a right triangle with the hypotenuse extending to the point (-7, -8).
The task is to find the sine of the angle \( \theta \), denoted as \( \sin \theta \).
**Diagram Explanation:**
1. **Coordinate System and Triangle:**
- The graph displays a quadrant of the Cartesian coordinate plane.
- A right triangle is formed with the origin (0, 0), the point (-7, -8), and the projection of this point onto the x-axis, which is (-7, 0).
2. **Points:**
- **Origin (0, 0):** Where the x and y axes intersect.
- **Point (-7, -8):** The terminal side of the angle passes through this point.
3. **Side Lengths of the Triangle:**
- Horizontal leg (adjacent to \( \theta \)): 7 units (from the x-projection to the point).
- Vertical leg (opposite to \( \theta \)): 8 units (from the y-projection).
4. **Hypotenuse:**
- Computed using the Pythagorean theorem:
\[
\text{hypotenuse} = \sqrt{(-7)^2 + (-8)^2} = \sqrt{49 + 64} = \sqrt{113}
\]
5. **Finding \( \sin \theta \):**
- The sine of the angle \( \theta \) is equal to the ratio of the length of the opposite side to the hypotenuse:
\[
\sin \theta = \frac{-8}{\sqrt{113}}
\]
**Note:**
- The negative sign in the sine function indicates the angle is below the x-axis, given its position in this quadrant of the circle.
**Interactive Portion:**
- A user input box for submitting the calculated value of \( \sin \theta \).
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning