an = 4n-²+2
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Hey,
I again have 2 sequences ( picture) i am not sure how to prove convergence for.
For the first one I tried the (ε, δ)-definition of limit but dont get anywhere with it.
Is it sufficient for the second one if i just calculate the limit (limes) of the sequence and therefore proove that its capped and as a result converges?
(ε, δ)
(ε, δ)
(ε, δ)-definition of limit

Transcribed Image Text:an = 4n-²+2

Transcribed Image Text:Cn
=
5n³ - n²
2n² +n³
n
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps with 2 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Thank you for your solution. It has been very helpful. Unfortunatly i struggle with the understanding:
1.) how/why does it go from 5n^3-n^2/2n^4+n^3 to 5n^3-n^2/2n^3+n^2 where does the n in the denominator go?
I also struggle with understanding the steps going from the term -5/2 to the term below. Can somebody explain it to me?
Thank you in Advance!
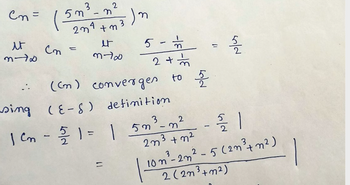
Transcribed Image Text:Cn=
사
30
...
13-32
234+m3
tm
Cn
5m
사
ตาม
n
곢
2+六
(cm) comvergen to 솜
5 -
=
wing (E-S) detimition
1cm - 2 1 = | 5m3-m²
233 + m²
(1
কান
세~
-
1
10m3-232-5 (2m3,m2)
2 (2n³+ m²)
3
1
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

