how that each of the following graphs are planar by providing a planar representation of the graph. e sure to label the vertices! (There is a good, free, online software program called Geogebra that you an use to help with this) (a) (b) (c) H F E G B E 0 E
how that each of the following graphs are planar by providing a planar representation of the graph. e sure to label the vertices! (There is a good, free, online software program called Geogebra that you an use to help with this) (a) (b) (c) H F E G B E 0 E
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:1. **Show that each of the following graphs are planar by providing a planar representation of the graph. Be sure to label the vertices! (There is a good, free, online software program called Geogebra that you can use to help with this)**
(a) The first graph consists of vertices labeled \( A, B, C, D, E, F, G \). All vertices are connected by various edges, including:
- Connections from \( A \) to \( B, C, D, E, F \)
- \( B \) connects to \( F, G \)
- \( D \) connects to \( C \)
- There is a zigzag pattern of connections from the top vertex \( C \) down to \( G \).
(b) The second graph is an octagon with vertices labeled \( A, B, C, D, E, F, G, H \).
- Each vertex on the perimeter is connected to its adjacent vertices creating an outer ring.
- Cross connections exist significantly within the shape:
- \( A \) directly connects to \( C, E \)
- \( B \) directly connects to \( D, F \)
- \( D \) connects to \( F \)
- Overall, creating a web of triangular connections within.
(c) The third graph forms a star with vertices labeled \( A, B, C, D, E, F, G, H \).
- The top point of the star is \( A \) connecting to \( B, C \).
- The five outer points \( B, C, D, E, F \) create star-shaped outer connections, enclosing a pentagon.
- The inside is criss-crossed with connections forming a smaller central pentagon formed by points \( B, C, D, E, F \) and \( H \).
These diagrams are used to illustrate different configurations and help determine if a given graph is planar, which means it can be drawn on a plane without any of its edges crossing, except at their endpoints.
Expert Solution
Step 1
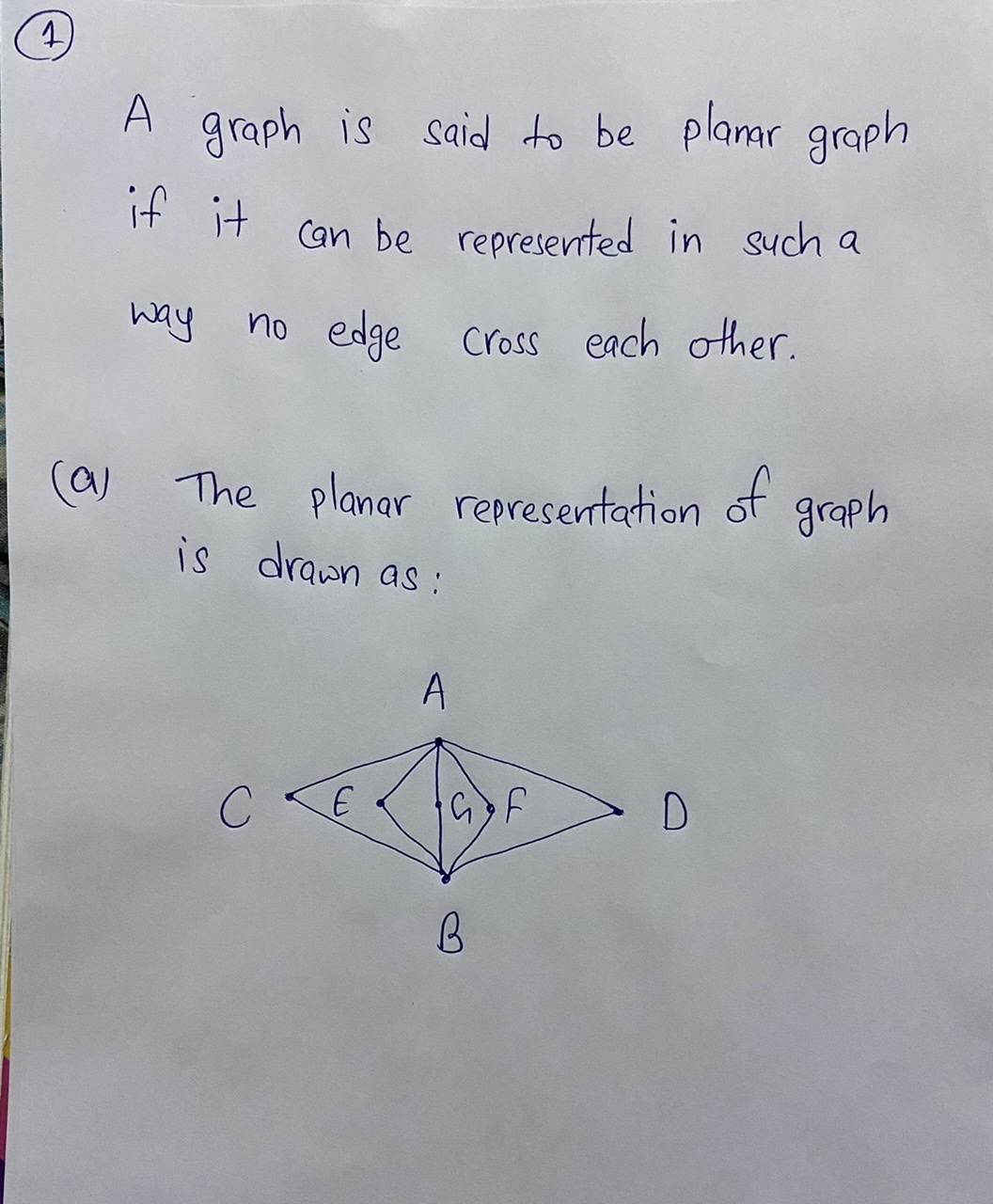
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

