Let R= {(x, e¹x) : xER, n = Z}. Here e = 2.71828... as usual.) Prove that R is an equivalence relation on the set of real umbers.
Let R= {(x, e¹x) : xER, n = Z}. Here e = 2.71828... as usual.) Prove that R is an equivalence relation on the set of real umbers.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:Let
R: = {(x,e¹x) : x ≤R,n≤ Z}.
Here e = 2.71828... as usual.) Prove that R is an equivalence relation on the set of real
umbers.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
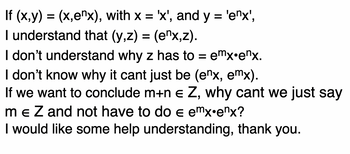
Transcribed Image Text:If (x,y) = (x,enx), with x = 'x', and y = 'enx',
I understand that (y,z) = (enx,z).
I don't understand why z has to = emx.ex.
I don't know why it cant just be (enx, emx).
If we want to conclude m+n € Z, why cant we just say
m € Z and not have to do e emx.enx?
E
I would like some help understanding, thank you.
Solution
Follow-up Question
hello, can you explain how it is symmetric in more detail?
Solution
Similar questions
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

