hand write, more details, Step by step solutions Spherical Charge System with Zero External Field: What spherical charge distribution creates the field given at right, where r is defined as in spherical coordinates? Note the discontinuity in the field: what does this require at the surface? E(T) = Porsa 380 0 r>a
hand write, more details, Step by step solutions Spherical Charge System with Zero External Field: What spherical charge distribution creates the field given at right, where r is defined as in spherical coordinates? Note the discontinuity in the field: what does this require at the surface? E(T) = Porsa 380 0 r>a
Related questions
Question
As soon as possible, Handwrite, more details please
Transcribed Image Text:hand write, more details, Step by step solutions
Spherical Charge System with Zero External Field: What
spherical charge distribution creates the field given at right,
where r is defined as in spherical coordinates? Note the
discontinuity in the field: what does this require at the
surface?
Porr r≤a
E(T) = 380
0
r>a
Expert Solution
Step 1
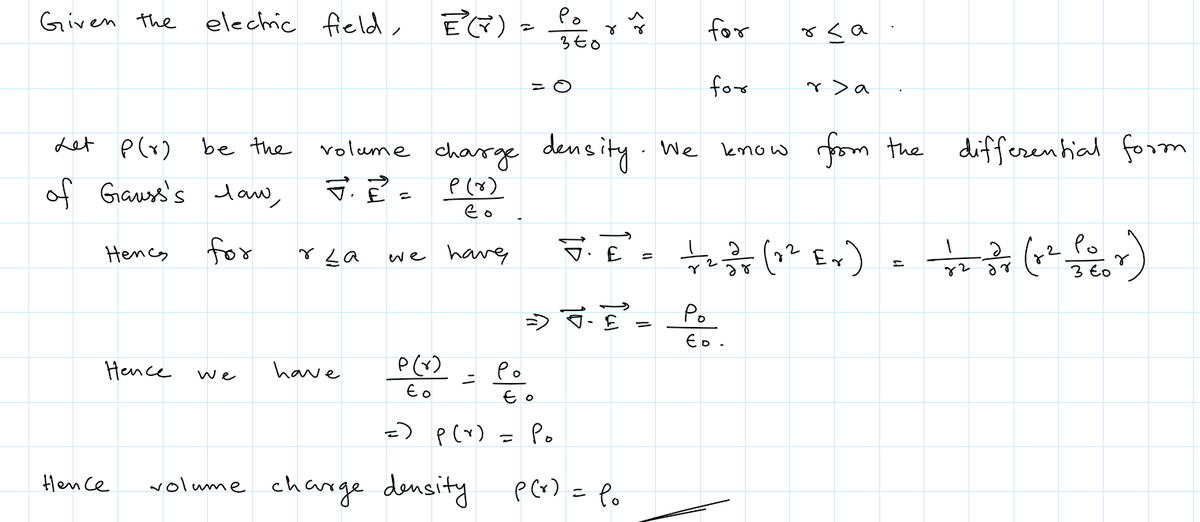
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images
