Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
Given that C₁ is defined by the circle x² + (y−1)² = 4 traced counterclockwise and C₂ be the trapezoid traced clockwise with vertices at (-5,3), (3,4), (3,-7) and (-5,-1). Consider the force field F(x, y) = (e¹-³ – 4y,4x −e²-³). a. By parametrizing C₁, find the work done by the force field F in moving an object around C₁ exactly once.

Given that C₁ is defined by the circle x² + (y−1)² = 4 traced counterclockwise and C₂ be the trapezoid traced clockwise with vertices at (-5,3), (3,4), (3,-7) and (-5,-1). Consider the force field F(x, y) = (e¹-³ – 4y,4x −e²-³). a. By parametrizing C₁, find the work done by the force field F in moving an object around C₁ exactly once.

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question
100%
Given that C₁ is defined by the circle x² + (y−1)² = 4 traced counterclockwise and C₂ be the trapezoid traced clockwise with vertices at (-5,3), (3,4), (3,-7) and (-5,-1). Consider the force field F(x,y)=(e--4y,4x-e²-). a. By parametrizing C₁, find the work done by the force field in moving an object around C₁ exactly once.
Transcribed Image Text:Given that C₁ is defined by the circle x² + (y−1)² = 4 traced counterclockwise and C₂ be the trapezoid traced clockwise with vertices at (-5,3), (3,4), (3,-7) and (-5,-1). Consider the force field F(x,y)=(e--4y,4x-e²-). a. By parametrizing C₁, find the work done by the force field in moving an object around C₁ exactly once.
Expert Solution
steps

Step by step

Solved in 4 steps

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

This is a continuation of the first question. See attached problem.

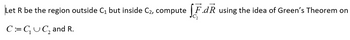
Let R be the region outside C₁ but inside C₂, compute F.dR using the idea of Green's Theorem on C:= C₁ C₂ and R.
Transcribed Image Text:Let R be the region outside C₁ but inside C₂, compute F.dR using the idea of Green's Theorem on C:= C₁ C₂ and R.
Solution
Bartleby Expert
SEE SOLUTION
Follow-up Question

Can you please write this solution ?

Use exponents and grouping symbol as well. Thank you. 

Solution
Bartleby Expert
SEE SOLUTION
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS