Give the rank and the nullity of the matrix. - [3 3] rank(A) nullity(A) A = = = 10-1 3 3
Give the rank and the nullity of the matrix. - [3 3] rank(A) nullity(A) A = = = 10-1 3 3
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Matrix Rank and Nullity Calculation**
*Problem Statement:*
Determine the rank and the nullity of the matrix \( A \).
*Matrix \( A \)*:
\[
A = \begin{bmatrix}
1 & 0 & -1 \\
3 & 3 & 3
\end{bmatrix}
\]
*Definitions*:
- **Rank of a Matrix**: The rank is the dimension of the column space (or row space) of the matrix. It represents the number of linearly independent columns.
- **Nullity of a Matrix**: The nullity is the dimension of the kernel (or null space) of the matrix. It represents the number of solutions to the homogeneous equation \( A\mathbf{x} = \mathbf{0} \) other than the trivial solution.
*Statement to Solve:*
- rank(A) = [ ]
- nullity(A) = [ ]
*Conceptual Explanation*:
- For a matrix with \( m \) columns, the rank and nullity are related by the equation: \[ \text{rank}(A) + \text{nullity}(A) = m \]
Please compute the required values for \( \text{rank}(A) \) and \( \text{nullity}(A) \) using these definitions and equations.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F992f5037-f1cc-4483-8aa3-731b184958ad%2F099b7259-f50f-43be-a8bf-fedc1ac68b94%2Frogesho_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Matrix Rank and Nullity Calculation**
*Problem Statement:*
Determine the rank and the nullity of the matrix \( A \).
*Matrix \( A \)*:
\[
A = \begin{bmatrix}
1 & 0 & -1 \\
3 & 3 & 3
\end{bmatrix}
\]
*Definitions*:
- **Rank of a Matrix**: The rank is the dimension of the column space (or row space) of the matrix. It represents the number of linearly independent columns.
- **Nullity of a Matrix**: The nullity is the dimension of the kernel (or null space) of the matrix. It represents the number of solutions to the homogeneous equation \( A\mathbf{x} = \mathbf{0} \) other than the trivial solution.
*Statement to Solve:*
- rank(A) = [ ]
- nullity(A) = [ ]
*Conceptual Explanation*:
- For a matrix with \( m \) columns, the rank and nullity are related by the equation: \[ \text{rank}(A) + \text{nullity}(A) = m \]
Please compute the required values for \( \text{rank}(A) \) and \( \text{nullity}(A) \) using these definitions and equations.
Expert Solution
Step 1: Reduce A to echelon form
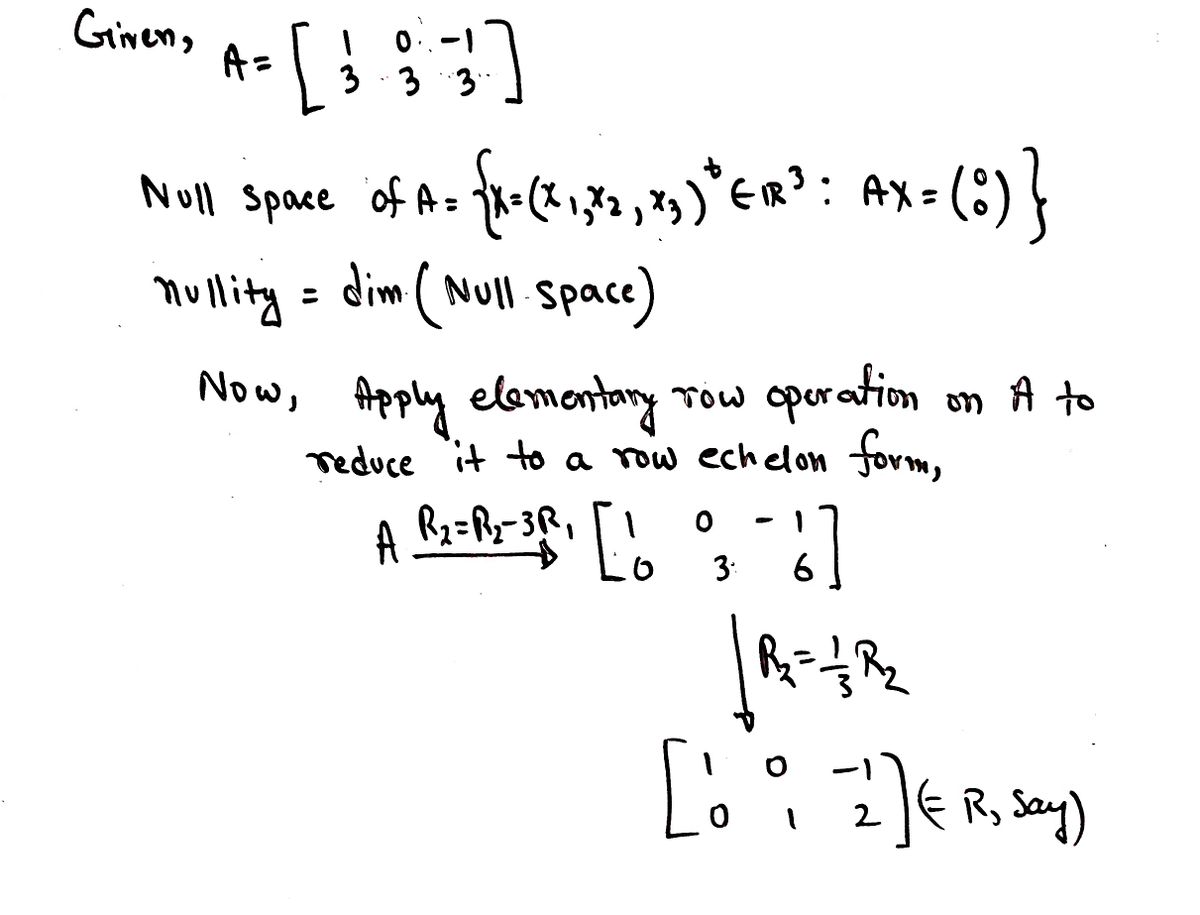
Step by step
Solved in 3 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

