Homework Help is Here – Start Your Trial Now!
Math
Geometry
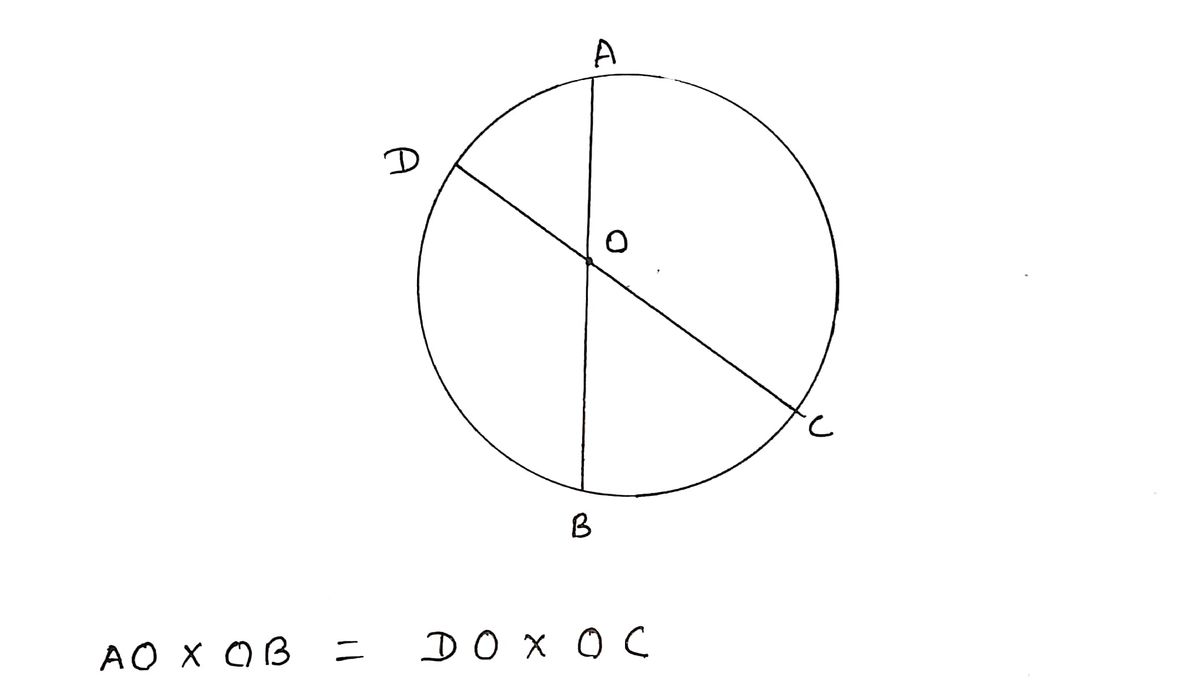
3 4 5 What is true when two chords intersect inside of a circle? The sum of the two lengths of one chord is always equal to the sum of the two lengths of the other chord O Their intersection MUST go through the center of the circle O The length of one chord is always equal to the length of another chord O The product of the two lengths of one chord is equal to the product of the two lengths of the other chord 2.

3 4 5 What is true when two chords intersect inside of a circle? The sum of the two lengths of one chord is always equal to the sum of the two lengths of the other chord O Their intersection MUST go through the center of the circle O The length of one chord is always equal to the length of another chord O The product of the two lengths of one chord is equal to the product of the two lengths of the other chord 2.

Elementary Geometry For College Students, 7e
Elementary Geometry For College Students, 7e
7th Edition
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.
ChapterP: Preliminary Concepts
SectionP.CT: Test
Problem 1CT
See similar textbooks
icon
Related questions
Question
3 4 5 What is true when two chords intersect inside of a circle? The sum of the two lengths of one chord is always equal to the sum of the two lengths of the other chord O Their intersection MUST go through the center of the circle O The length of one chord is always equal to the length of another chord O The product of the two lengths of one chord is equal to the product of the two lengths of the other chord 2.
Transcribed Image Text:3 4 5 What is true when two chords intersect inside of a circle? The sum of the two lengths of one chord is always equal to the sum of the two lengths of the other chord O Their intersection MUST go through the center of the circle O The length of one chord is always equal to the length of another chord O The product of the two lengths of one chord is equal to the product of the two lengths of the other chord 2.
Expert Solution
Step 1

Geometry homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer