G3 (a) Which of the previous graphs have a Hamiltonian path? (b) Which of the previous graphs have a Hamiltonian cycle? (c) Which of the previous graphs have an Eulerian trail? (d) Which of the previous graphs have an Eulerian circuit? GA
G3 (a) Which of the previous graphs have a Hamiltonian path? (b) Which of the previous graphs have a Hamiltonian cycle? (c) Which of the previous graphs have an Eulerian trail? (d) Which of the previous graphs have an Eulerian circuit? GA
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

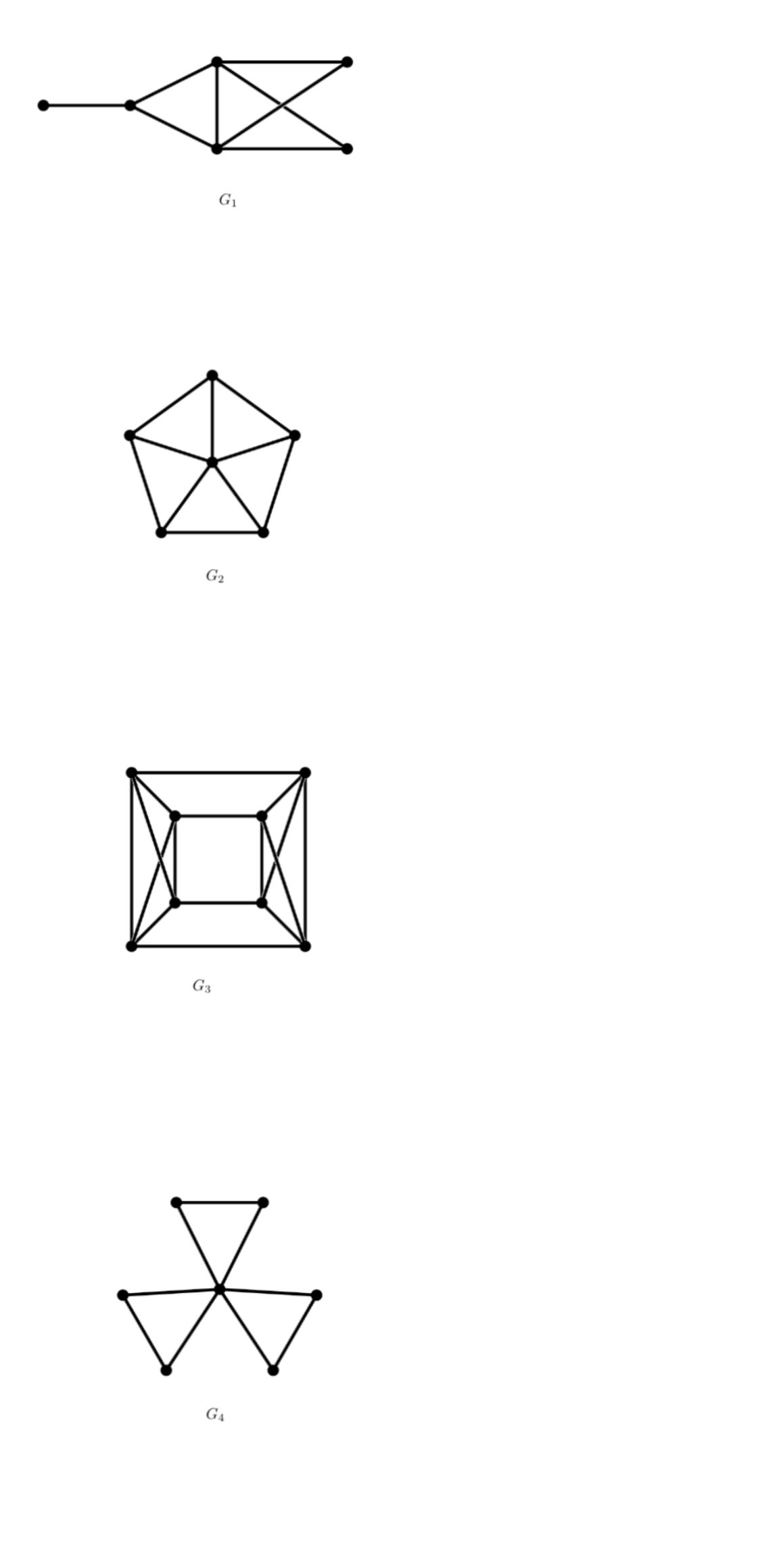
Transcribed Image Text:### 1. Consider the following graphs.
#### Graph Descriptions:
- **Graph \( G_1 \):**
- It is a simple graph with a horizontal line at the bottom extending into two triangles that share a common vertex.
- The triangles form a shape resembling a kite or two adjacent triangles, with one additional edge connecting the outer vertices of the triangles.
- **Graph \( G_2 \):**
- This graph is a complete pentagon with diagonals drawn, forming a star-like pattern inside the pentagon.
- All vertices of the pentagon are connected, creating a complete graph \( K_5 \).
- **Graph \( G_3 \):**
- A 3D cube projection or cube-like structure known as a graph cube.
- It consists of a central square with additional edges connecting adjacent vertices to form a cube structure.
- **Graph \( G_4 \):**
- A graph consisting of two triangles sharing a common vertex.
- The two base vertices of each triangle are not connected directly to each other, forming a vertical axis symmetry.
#### Questions:
(a) Which of the previous graphs have a Hamiltonian path?
(b) Which of the previous graphs have a Hamiltonian cycle?
(c) Which of the previous graphs have an Eulerian trail?
(d) Which of the previous graphs have an Eulerian circuit?
Explore these properties in each graph to further your understanding of these fundamental concepts in graph theory.
Expert Solution
Step 1

Step by step
Solved in 2 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

