For two samples, sample size n, sample mean , and the standard deviation of the population o where the sample has come are given as follows. from n= 64 = 490 feet, o = 12 feet ーu %3D n= 100 x = 168 kg , o = 9 kg %3D b) Discuss Null and Alternative hypothesis and explain two types of errors in the testing of Hypotheses. P,> P2 (04marks) Ha.= P P2 For each sample, estimate the population mean at 95% confidence level. ) (04marks)

The data on two samples are given in the problem. Both the samples are drawn from the distinct populations since both the sample statistics have different units, feet and kg. We cannot test the equality of means for these populations.
The given information is insufficient to carry out the hypothesis test since the claim is not specified.
But we can construct 95% confidence intervals for both the population means separately. This gives an estimate of the population mean at 95% confidence level. Therefore, the solution for part B is given as follows.
We have,
(a). n = 64, x.bar = 490 feet, σ = 12 feet.
(b). n = 100, x.bar = 168 kg, σ = 9 kg.
Since the population standard deviation, σ is know for both the populations, we use Z interval to find the 95% confidence intervals for population means. The formula for confidence interval for population mean, µ, is given by;
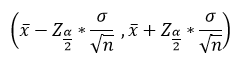
Where Z(α/2) is the critical value for confidence interval.
Here for 95% confidence interval, we get α = 0.05.
The right tailed probability to the upper critical value Z(0.025) is 0.025. Hence the left tailed probability to the upper critical value Z(0.025) is (1-0.025=) 0.975. Also the Z table gives the left tailed probabilities for given Z score. Using the Z table we get, Z(0.025) = 1.96.
Step by step
Solved in 3 steps with 3 images









