Homework Help is Here – Start Your Trial Now!
Math
Algebra
For the table in below. Identify the y-intercept and explain how you know X 1 2 W|N 3 4 Y 2 -3 -8 -13

For the table in below. Identify the y-intercept and explain how you know X 1 2 W|N 3 4 Y 2 -3 -8 -13

Algebra and Trigonometry (6th Edition)
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
See similar textbooks
icon
Related questions
Question

The image provided below will help.

**Understanding Linear and Quadratic Equations through Differences** 1. **Linear Equations**: - **Definition**: When the first differences are the same, it indicates a linear equation. - **Characteristics**: - The first differences are equal to the slope, \(m\). - **General Equation**: \(f(x) = mx + b\). 2. **Quadratic Equations**: - **Definition**: When the second differences are the same, it indicates a quadratic equation. - **Characteristics**: - Second differences are equal to \(2a\). - **Finding "a"**: Divide the second differences by 2. - **General Equation**: \(f(x) = ax^2 + bx + c\). - **Intercept**: \(c\) is the y-intercept. These principles allow for the identification and formulation of equations based on the patterns in their differences.
Transcribed Image Text:**Understanding Linear and Quadratic Equations through Differences** 1. **Linear Equations**: - **Definition**: When the first differences are the same, it indicates a linear equation. - **Characteristics**: - The first differences are equal to the slope, \(m\). - **General Equation**: \(f(x) = mx + b\). 2. **Quadratic Equations**: - **Definition**: When the second differences are the same, it indicates a quadratic equation. - **Characteristics**: - Second differences are equal to \(2a\). - **Finding "a"**: Divide the second differences by 2. - **General Equation**: \(f(x) = ax^2 + bx + c\). - **Intercept**: \(c\) is the y-intercept. These principles allow for the identification and formulation of equations based on the patterns in their differences.
**Identifying the Y-Intercept from a Data Table** In the following table, we have pairs of X and Y values. Our task is to identify the y-intercept and explain the process. | X | Y | |---|----| | 1 | 2 | | 2 | -3 | | 3 | -8 | | 4 | -13| **Explanation:** The y-intercept is the point where a line crosses the Y-axis, which occurs when X = 0. The given table does not provide a Y value for X = 0, so we need the equation of the line to find the y-intercept. 1. **Determine the Equation of the Line:** - First, calculate the slope (m) using the formula: \[ m = \frac{Y_2 - Y_1}{X_2 - X_1} \] Using points (1, 2) and (2, -3): \[ m = \frac{-3 - 2}{2 - 1} = \frac{-5}{1} = -5 \] 2. **Using the Slope-Intercept Form:** - The slope-intercept form of a line is: \[ Y = mX + b \] Using point (1, 2) and slope -5: \[ 2 = -5(1) + b \] \[ 2 = -5 + b \implies b = 7 \] 3. **Conclusion:** - The y-intercept (b) is 7. Thus, the line crosses the Y-axis at (0, 7). Understanding how to derive the equation from the table and find the y-intercept helps in comprehending linear relationships and graph interpretation.
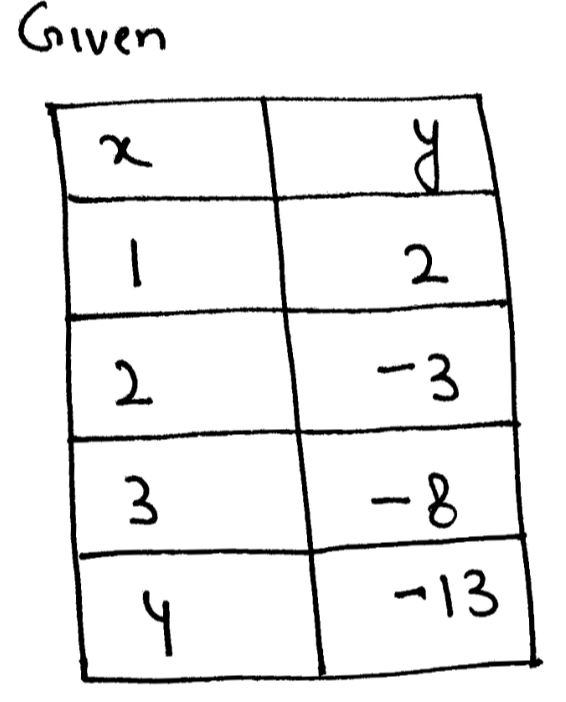
Transcribed Image Text:**Identifying the Y-Intercept from a Data Table** In the following table, we have pairs of X and Y values. Our task is to identify the y-intercept and explain the process. | X | Y | |---|----| | 1 | 2 | | 2 | -3 | | 3 | -8 | | 4 | -13| **Explanation:** The y-intercept is the point where a line crosses the Y-axis, which occurs when X = 0. The given table does not provide a Y value for X = 0, so we need the equation of the line to find the y-intercept. 1. **Determine the Equation of the Line:** - First, calculate the slope (m) using the formula: \[ m = \frac{Y_2 - Y_1}{X_2 - X_1} \] Using points (1, 2) and (2, -3): \[ m = \frac{-3 - 2}{2 - 1} = \frac{-5}{1} = -5 \] 2. **Using the Slope-Intercept Form:** - The slope-intercept form of a line is: \[ Y = mX + b \] Using point (1, 2) and slope -5: \[ 2 = -5(1) + b \] \[ 2 = -5 + b \implies b = 7 \] 3. **Conclusion:** - The y-intercept (b) is 7. Thus, the line crosses the Y-axis at (0, 7). Understanding how to derive the equation from the table and find the y-intercept helps in comprehending linear relationships and graph interpretation.
Expert Solution
Step 1

Algebra homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Algebra and Trigonometry (6th Edition)
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON
Contemporary Abstract Algebra
Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning
Linear Algebra: A Modern Introduction
Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON
Introduction to Linear Algebra, Fifth Edition
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press
College Algebra (Collegiate Math)
College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education
SEE MORE TEXTBOOKS