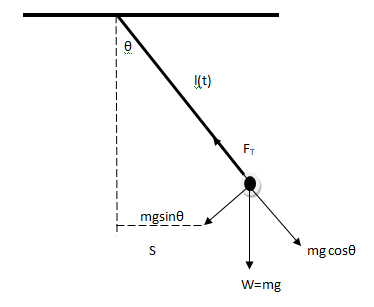
For the flat pendulum in the figure: Determine the binding forces in the case that L is constant
Q: A simple pendulum of length and bob with mass m is attached to a massless support moving vertically…
A: Given: A simple pendulum having length of string, λ Mass of bob is m and Constant acceleration, α…
Q: P341: Consider the one-dimensional potential -(22 +1) U(2) = 4+8 Sketch the potential and discuss…
A: Required : Plot of the potential.
Q: A pendulum which drops sand as it swings back and forth is shown. This pendulum has been swinging…
A: The objective of the question is to understand the reason behind the change in direction of the…
Q: Table 1: Static (non-oscillatory) force-displacement data for determining the spring constant of the…
A: SOlution: to find the value for the given blans in the columns
Q: A particle of mass m is located at a one-dimensional potential, a b U(x) x2 - Where the period of…
A:
Q: The net x-force on a 1-kg oscillating object moving along the x axis is Fx = −b(x − a2x3), where b =…
A: (given) Fx=-b(x-a2x3) b= 123 x a=4 y The unit of "a2x3"should be "m" a2[m23] = m…
Q: Problem 4: A particular spring does not obey Hooke's law (F(x) = -k x), but rather is described by…
A:
Q: There are three particles of mass m connected to each other and to the walls by (light) springs as…
A: A) Newton's 2nd law for each particle is written as (in the order from left to right):…
Q: Mass is attached to a spring and set to oscillate horizontally on a frictionless surface. At what…
A: As per our guidelines, we are supposed to answer only first three subparts in case of multiple…
Q: (b) A particle moves from position A to position B in the following Cartesian coordinate system.…
A: We are given 2 points in space. We first find position vectors of these 2 points. We then find the…
Q: R string R string 2m m Case 2 Case 1 2v 2R
A: The mathematical formula to calculate the time period is given as, T=2πrv Here, v is velocity and r…
Q: Using small angle how do I get the frequency
A:
Q: (e) We now consider the new system shown in the bottom figure. The mass m₂ in the right hand side is…
A:
Q: 4t Suppose you have a harmonic oscillator whose displacement from the equilibrium position is given…
A: Let y’(t) and y”(t) denote the first and second-order derivative of the given function y(t).
Q: The spring is then place sideways on a frictionless table attached to a 0.8 kg mass. It is set into…
A:
Q: A drill bit is able to reach 2000 rpm in 0.50 s. Assuming a constant angular acceleration, how many…
A: Given: The final angular speed of the drill is dω=2000 rpm= 2000×2π60 s=209.44 rads. Time required…
Q: Jack and Jill are playing with a tire swing tied to a tree branch. Jack is standing on one side of…
A: Tire swing completes one complete oscillation when it starts from jack and moves to Jill and then…
Q: A magnesium atom (mass of ~ 24 proton masses) in a crystal is measured to oscillate with a frequency…
A: Mass of Mg atom = mass of 24 protonWe know mass of 1 proton = 1.67 kgMass of Mg atom is (m) = =…
Q: 9. Solve the coupled oscillator system such that m₁ = m² = 1, k₁ = k3 = 9,k₂ = 8. Assume the first…
A: The objective of the question is to solve a coupled oscillator system and describe the behavior of…
Q: By using hamiltonian equations. Find the solution of harmonic oscillator in : A-2 Dimensions B-3…
A: For a Harmonic oscillator, the Kinetic energy T and Potential Energy V are given by, Considering…
Q: An m-mass pendulum is connected to a spring with the spring constant k through the massless rope…
A: Given that the mass of pendulum bob is m, the spring has a spring constant k, the equilibrium length…
For the flat pendulum in the figure:
Determine the binding forces in the case that L is constant
Note: constraint functions
r=L
f1= r-L
Z=0
f2=Z

Step by step
Solved in 3 steps with 1 images

- If the period of a pendulum on another planet is four times its period measured on Earth, what is the gravitational acceleration on the planet? Show the equation used and your calculations.9. Solve the coupled oscillator system such that m₁ = m² = 1, k₁ = k3 = 9,k₂ = 8. Assume the first mass is pushed 2 units to the right of equilibrium and the 2nd 2 units to the left of equilibrium, with zero initial velocities. Describe the behavior of the motions of the masses at each of the nodes.A spring with a spring constant of k=157N/m is initially compressed by a block a distance d=0.21m. The block is on horizontal surface with coefficient of kinetic friction yk static friction ys and has a mass of m=6kg B)Assuming the block is released from the initial position and begins to move to the right input an expression for the sum of the force in the x- direction in the configuration.
- Which of the following statements is true for the pendulum bob pictures in the figure? A O UA+UE=Kc O UA-2Kc O UD-KC UA-KE O UA-KC C D EHow do you do the last one ? ( it’s not 24.4 or 25)Three children are riding on the edge of a merry-go-round that is a disk of mass 98 kg, radius 1.9 m, and is spinning at 25rpm. The children have masses of 24 kg, 26 kg, and 32.6 kg.Randomized VariablesM = 98 kgm1 = 24 kgm2 = 26 kgm3 = 32.6 kgr = 1.9 mf = 25 rpm If the child who has a mass of 26 kg moves to the center of the merry-go-round, what is the new magnitude of angular velocity in rpm? f' =