Find the vector equation for the line of intero section of the planes 32-3y + 4z =-5 and X + 5z =0 +=([1₁7], 0) x² + +(-15, 0], [D
Find the vector equation for the line of intero section of the planes 32-3y + 4z =-5 and X + 5z =0 +=([1₁7], 0) x² + +(-15, 0], [D
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Can anyone please help me to solve this problem? I am stuck!
![**Topic: Finding the Vector Equation for the Line of Intersection of Two Planes**
To find the vector equation of the line where two planes intersect, consider the given planes:
1. Plane 1: \( 3x - 3y + 4z = 5 \)
2. Plane 2: \( x + 5z = 0 \)
The line of intersection of the two planes can be determined using a vector equation expressed as:
\[
\mathbf{r} = \langle 0, 0, 2 \rangle + t \langle 5, 0, 3 \rangle
\]
Here, \(\mathbf{r}\) denotes the position vector of any point on the line. It is composed of a point on the line, \(\langle 0, 0, 2 \rangle\), and a direction vector, \(\langle 5, 0, 3 \rangle\), scaled by the parameter \(t\).
This parameter \(t\) can take any real number value, representing the line's extension in both directions along the vector \(\langle 5, 0, 3 \rangle\).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F99d15f92-0bff-4b4d-a47e-2ac33d144271%2F140e11ba-0bad-4ff3-9252-e1db40292812%2Ftlwpk7g_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Topic: Finding the Vector Equation for the Line of Intersection of Two Planes**
To find the vector equation of the line where two planes intersect, consider the given planes:
1. Plane 1: \( 3x - 3y + 4z = 5 \)
2. Plane 2: \( x + 5z = 0 \)
The line of intersection of the two planes can be determined using a vector equation expressed as:
\[
\mathbf{r} = \langle 0, 0, 2 \rangle + t \langle 5, 0, 3 \rangle
\]
Here, \(\mathbf{r}\) denotes the position vector of any point on the line. It is composed of a point on the line, \(\langle 0, 0, 2 \rangle\), and a direction vector, \(\langle 5, 0, 3 \rangle\), scaled by the parameter \(t\).
This parameter \(t\) can take any real number value, representing the line's extension in both directions along the vector \(\langle 5, 0, 3 \rangle\).
![**Problem Statement:**
Find the vector equation for the line of intersection of the planes:
\[ 3x - 3y + 4z = -5 \]
and
\[ x + 5z = 3 \]
**Solution:**
The vector equation for the line is given by:
\[ \mathbf{r} = \langle 0, 0, 0 \rangle + t \langle -15, 0, 3 \rangle \]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F99d15f92-0bff-4b4d-a47e-2ac33d144271%2F140e11ba-0bad-4ff3-9252-e1db40292812%2Fw2ukipji_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Find the vector equation for the line of intersection of the planes:
\[ 3x - 3y + 4z = -5 \]
and
\[ x + 5z = 3 \]
**Solution:**
The vector equation for the line is given by:
\[ \mathbf{r} = \langle 0, 0, 0 \rangle + t \langle -15, 0, 3 \rangle \]
Expert Solution
Step 1
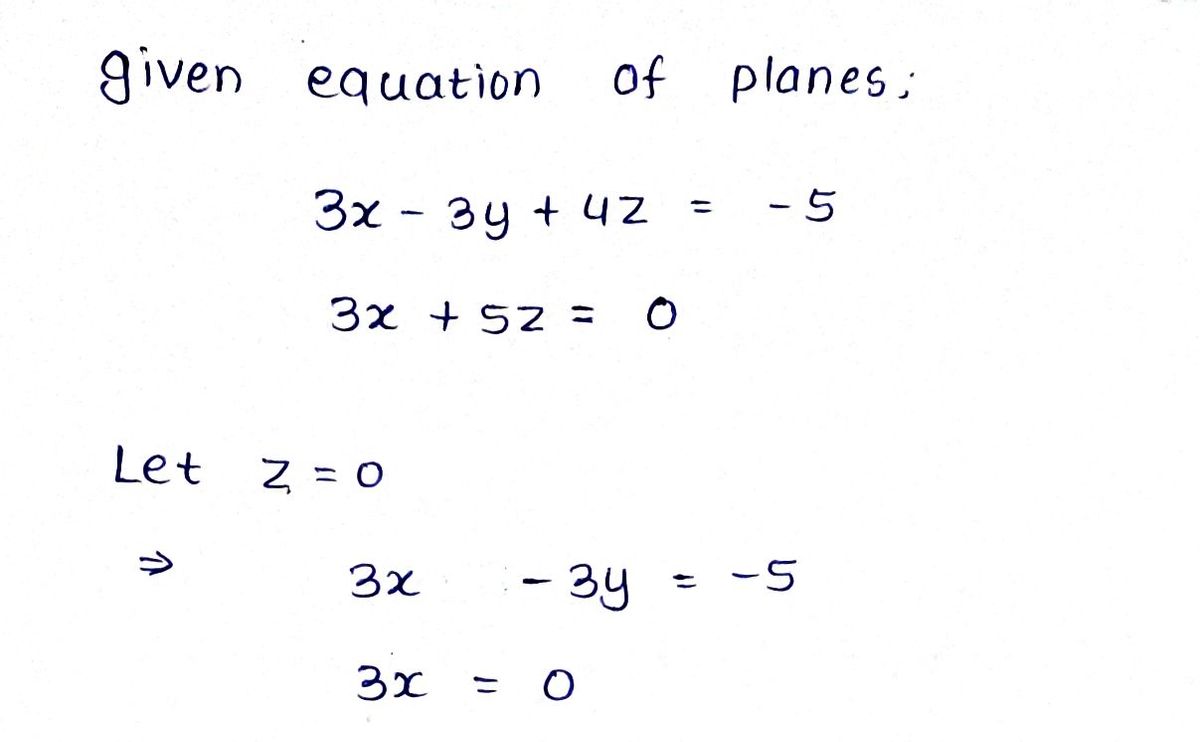
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

